El problema de Euler de los tres cuerpos
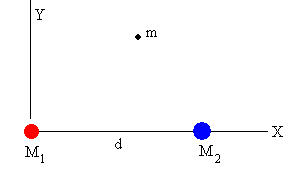 El movimiento de dos masas puntuales bajo la acción de
la fuerza de atracción mutua es un problema simple: Los dos cuerpos se
mueven en órbitas elípticas alrededor de su centro de masas. El movimiento
de tres cuerpos es muy complejo.
El movimiento de dos masas puntuales bajo la acción de
la fuerza de atracción mutua es un problema simple: Los dos cuerpos se
mueven en órbitas elípticas alrededor de su centro de masas. El movimiento
de tres cuerpos es muy complejo.
El problema de Euler de los tres cuerpos, es un sistema formado por dos cuerpos de gran masa fijos en el espacio, separados una distancia d, y una partícula de pequeña masa m que se mueve en el espacio circundante. Este problema se puede resolver analíticamente, pero es bastante complicado.
En esta página, se plantean las ecuaciones del movimiento y se resuelven aplicando procedimientos numéricos.
Ecuaciones del movimiento
Los cuerpos fijos en el espacio tiene masas M1 y M2, y están separados una distancia d. Estableceremos un Sistema de Referencia, con el origen en el primer cuerpo, y el eje X es la recta que une sus centros, tal como se muestra en la figura.
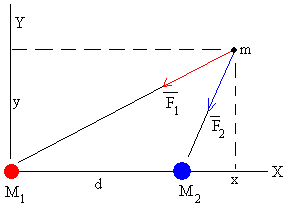
Cuando la partícula se encuentra en la posición (x, y), las fuerzas de atracción que ejerce cada uno de los cuerpos sobre la pequeña partícula se muestran en la figura, sus módulos valen
Descomponemos las fuerzas. Las ecuaciones del movimiento de la partícula de masa m son:
Tenemos un sistema de dos ecuaciones diferenciales de segundo orden
Que se resuelven por procedimientos numéricos con las condiciones iniciales siguientes: En el instante t=0, la partícula se encuentra en la posición (x0, y0) y las componentes de su velocidad inicial son, (v0x, v0y).
Escalas
Antes de resolver el sistema de ecuaciones diferenciales por procedimientos numéricos, es conveniente prepararlas para que el ordenador no maneje números excesivamente grandes o pequeños.
Establecemos un sistema de unidades en el que la longitud se mide en unidades astronómicas, la distancia media entre el Sol y la Tierra. L=una UA=1.496·1011 m y el tiempo en unidades de año, P=un año= 365.26 días=3.156·107 s.
Supongamos el primer cuerpo es el Sol, M1= 1.98·1030 kg y la masa del segundo cuerpo es un múltiplo de la masa del Sol, M2=αM1
En el nuevo sistema de unidades x=Lx', t=P·t', la primera ecuación diferencial se escribe
y de forma similar la segunda ecuación diferencial.
Como L es el semieje mayor de la órbita de la Tierra alrededor del Sol, P es el periodo o tiempo que tarda en dar una vuelta completa, y M1 es la masa del Sol. Por la tercera ley de Kepler, el término
Volviendo a la notación previa: x e y para la posición y t para el tiempo en el nuevo sistema de unidades. El sistema de ecuaciones diferenciales se escribe
Se resuelve este sistema de ecuaciones diferenciales por el procedimiento de Runge-Kutta, con un paso variable. Este paso se ha elegido de modo que cuando la partícula está alejada de los cuerpos fijos el paso es grande y cuando está cerca de alguno de los dos cuerpos el paso es pequeño.
Principio de conservación de la energía
La energía total de la partícula es una constante del movimiento.
La energía de la partícula de masa m en el instante inicial t=0 es
Cuando E0<0 la partícula permanece confinada en el espacio que rodea a los dos cuerpos. Cuando E0≥0 la partícula escapa al infinito
La energía de la partícula en el instante t es igual a
En el nuevo sistema de unidades establecido, las magnitudes velocidad y posición están relacionadas del siguiente modo:
v=v’·L/P, x=x’·L, y=y’·L, d=d’·L
Volviendo a la notación previa. Definimos una nueva energía e por unidad de masa en este sistema de unidades
El programa interactivo evalúa en cada instante el cociente
que denominaremos tanto por ciento de error. Cuando la energía e difiere de e0 de modo que el cociente es mayor que la unidad, el programa interactivo se detiene, la trayectoria calculada puede que se desvíe significativamente de la real.
Actividades
Se introduce
-
El parámetro α=M2/M1, donde M1 es la masa del Sol, en el control de edición titulado C. masas.
-
La distancia d entre los dos cuerpos fijos, en el control de edición titulado Distancia.
-
La posición inicial (x0, y0), en los dos controles de edición titulados Posición
-
La velocidad inicial (v0x, v0y), en los dos controles de edición titulados Velocidad
Se pulsa el botón titulado Empieza
Se observa la trayectoria de la partícula de masa m. En la parte derecha, se proporcionan los datos de su posición (x, y) y de su velocidad (vx, vy) en cada instante t.
En la parte inferior derecha, se muestra en color rojo el tanto por ciento de error. Cuando es mayor que la unidad el programa interactivo se detiene. Como podemos comprobar, los mayores porcentajes de error se obtienen cuando la partícula pasa muy cerca de alguno de los dos cuerpos fijos.
Nota: Se ha de advertir al lector, que como el paso de integración de las ecuaciones diferenciales del movimiento es variable, la velocidad del punto que representa la partícula en el applet, no se corresponde con la velocidad real de la partícula.
Se aconseja probar los siguientes ejemplos:
Ejemplo 1
-
Los dos cuerpos tienen la misma masa, α=1.0
-
La distancia fija entre los dos cuerpos, d=2.1,
-
Posición inicial, x0=1, y0=0
-
Velocidad inicial v0x=0, v0y=6.28
Ejemplo 2
-
Los dos cuerpos tienen la misma masa, α=1.0
-
La distancia fija entre los dos cuerpos, d=0.2,
-
Posición inicial, x0=1, y0=0
-
Velocidad inicial v0x=0, v0y=6.28
Ejemplo 3
-
Los dos cuerpos tienen la misma masa, α=1.0
-
La distancia fija entre los dos cuerpos, d=3.0,
-
Posición inicial, x0=1.5, y0=0
-
Velocidad inicial v0x=3, v0y=3
Referencias
Wild W. J. Euler's three-body problem. Am. J. Phys. 48(4) April 1980, pp. 297-301
