Trayectorias hiperbólicas
Los planetas describen órbitas elípticas, en uno de cuyos focos está situado el Sol. Las trayectorias elípticas son las más comunes de los cuerpos celestes y así, serán estudias en este capítulo. Las trayectorias hiperbólicas son más raras, aparecerán en la página titulada “Encuentro de una sonda espacial con el planeta Júpiter” y sobre todo, en el estudio del fenómeno de la dispersión en el capítulo Mecánica Cuántica.
Descripción
Supongamos que un asteroide de masa m se aproxima a un planeta de masa M con velocidad v0 en el infinito siguiendo una dirección (recta de color rojo) que dista b del centro del planeta tal como se muestra en la figura. A medida que el asteroide se acerca al planeta, va cambiando su velocidad tanto en módulo como en dirección (en color azul), hasta que se aleja hacia el infinito siguiendo una dirección simétrica respecto del eje X, que es la asíntota de la otra rama de la hipérbola.
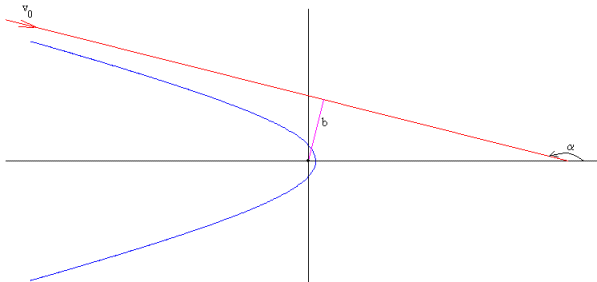
Para analizar el problema supondremos que la masa del asteroide es muy pequeña comparada con la del planeta, m<<M y no tendremos en cuenta la influencia del Sol ni la del resto del los planetas.
La ecuación de la trayectoria es
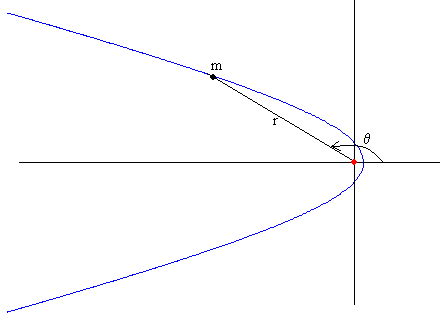
r es la distancia del centro del planeta al asteroide y θ es el ángulo que hace el radio vector que une el asteroide con el centro del planeta con el eje X, tal como se ha mostrado en la figura.
El parámetro ε denominado excentricidad define el tipo de trayectoria. La trayectoria es una hipérbola si ε>1 es decir, si la energía del asteroide E>0.
La energía del asteroide en el infinito es solamente cinética
El momento angular es
L=mv0b
Los parámetros ε y d valen
La distancia más cercana del asteroide al centro del planeta ocurre cuando θ=0
Esta distancia la podemos calcular aplicando la conservación de la energía y del momento angular en el punto P más cercano al centro del planeta.
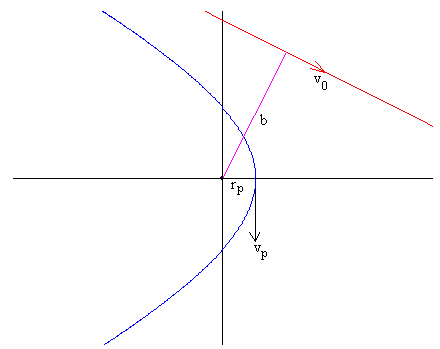
En este sistema de dos ecuaciones con dos incógnitas despejamos vp y rp
Dependiendo de las magnitudes M, v0, b y el radio R del planeta el asteroide choca rp<R o pasa el planeta. Cuando rp=R el asteroide choca tangencialmente con el planeta.
Asíntotas
El ángulo para el cual r→∞, es
La dirección de la velocidad del asteroide cambia a medida que se acerca al planeta y luego, cuando se aleja. El cambio en la dirección de la velocidad es 2α-180 tal como se aprecia en la figura.
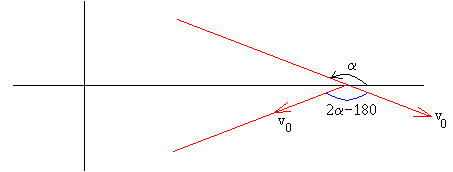
La asíntota de una de las ramas de la hipérbola hace un ángulo α con el eje X y dista b del origen como podemos ver en la figura.
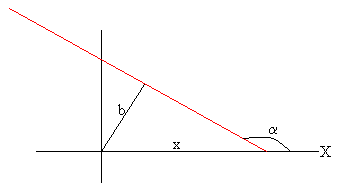
Interseca al eje X en la posición x
Actividades
Se elige un planeta en el control de selección titulado Planeta
Se introduce
-
La velocidad v0 del asteroide en el infinito en km/s, en el control de edición titulado Velocidad
-
El parámetro de impacto en unidades del radio del planeta actuando en la barra de desplazamiento titulada Parámetro de impacto
Se pulsa el botón titulado Empieza
La trayectoria del asteroide empieza a dibujarse a una distancia r=10·R, diez veces el radio del planeta. En la parte superior derecha del applet, se nos proporciona los datos del tiempo en horas y la distancia en radios del planeta elegido.
Se sugiere al lector:
-
Que elija un planeta en la lista, mantenga fija la velocidad v0, y cambie el parámetro de impacto, distinguiendo las trayectorias que hacen que el asteroide choque con el planeta de aquellas en las que pasa.
-
Que calcule la excentricidad de la órbita, y la intersección x de la asíntota con el eje horizontal en unidades del radio del planeta.
Datos
| Planeta | GM | Radio (km) |
| Tierra | 3.986·1014 | 6378 |
| Marte | 4.283·1013 | 3397 |
| Júpiter | 1.267·1017 | 71 492 |
| Saturno | 3.793·1016 | 60 268 |
Referencias
Van Allen J. A., Encounter of an asteriod with a planet. Am. J. Phys. 74 (8) August 2006, pp. 717-719
