Movimiento bajo una fuerza central y una perturbación
En esta página, estudiaremos el problema del movimiento bajo una fuerza central y conservativa inversamente proporcional al cuadrado de la distancia al centro de fuerzas, y una perturbación que corresponde a una fuerza inversamente proporcional al cubo de la distancia. Obtendremos explícitamente la ecuación de la trayectoria en coordenadas polares, y las representaremos para todos los casos posibles: fuerza atractiva o repulsiva combinada con una perturbación atractiva o repulsiva. Consideraremos también el caso en el que la perturbación es nula.
Fuerza central y conservativa
Cuando un móvil está sometido a una fuerza central y conservativa, se mantiene constante el momento angular y la energía total de la partícula.
Para obtener la ecuación explícita de la trayectoria, expresaremos las distintas magnitudes en coordenadas polares. Supongamos que la partícula se mueve en una región cuya energía potencial V(r) solamente depende de la distancia r al centro de fuerzas.
En coordenadas polares la energía total se escribe
El momento angular se escribe
Introduciendo la segunda ecuación en la primera, obtenemos
Decimos que la partícula se mueve en una región unidimensional r>0 bajo un potencial efectivo
Si la fuerza es repulsiva la energía total solamente puede ser positiva. Supongamos que la energía de la partícula vale E>0.
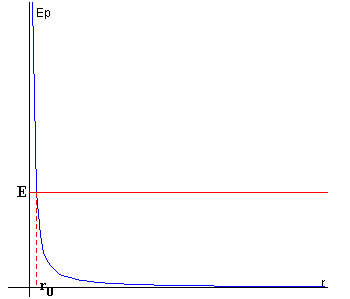 |
En la representación de la energía potencial efectiva, trazamos una recta horizontal de ordenada E. Sea r0 la abscisa que corresponde al punto de intersección de la recta horizontal y la curva de energía potencial. Teniendo en cuenta que la región en la que puede moverse una partícula es aquella en la que su energía cinética es positiva o nula, el movimiento de la partícula se extenderá desde r0 a infinito. |
Una partícula procedente del infinito se acercará al centro de fuerzas hasta una distancia r0 y regresará de nuevo al infinito.
Si la fuerza es atractiva la energía de la partícula puede ser positiva o negativa. El valor de la energía total no puede ser menor que el mínimo de la energía potencial efectiva.
Si la energía de la partícula es positiva su movimiento no está limitado, del mismo modo que para el caso de fuerzas repulsivas una partícula procedente del infinito se puede acercar hasta una distancia r0 del centro de fuerzas para alejarse posteriormente de dicho centro.
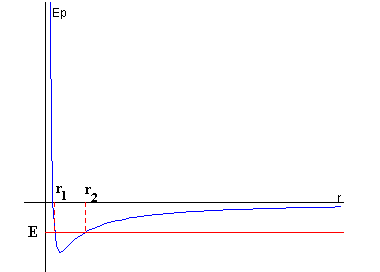 |
El caso más interesante se produce cuando la energía de la partícula es negativa, tal como se señala en la figura. El movimiento de dicha partícula está limitado a una región radial comprendida entre r1 y r2, que son las abscisas de los puntos intersección de la recta horizontal y la curva de energía potencial, el primero corresponde al perihelio (o perigeo) la distancia de máximo acercamiento de la partícula al centro de fuerzas, el segundo al afelio (o apogeo) distancia de máximo alejamiento del móvil al centro de fuerzas. |
Las ecuaciones y de constancia del momento angular y de la energía constituyen un par de ecuaciones diferenciales en las que se puede eliminar el tiempo t, para obtener la ecuación de la trayectoria r=r(θ) integrado la ecuación diferencial
Fuerza inversamente proporcional al cuadrado de la distancia
Si la fuerza que actúa sobre la partícula es central y conservativa inversamente proporcional al cuadrado de la distancia r al centro de fuerzas,
el resultado de la integración de (1) es la ecuación de una cónica.
Los parámetros d y ε están relacionados con la energía y el momento angular del siguiente modo
Para una fuerza atractiva (α<0) el tipo de cónica viene determinado por el valor y signo de la energía.
| Excentricidad | Energía | Trayectoria |
| ε>0 | E>0 | hipérbola |
| ε=0 | E=0 | parábola |
| ε<0 | E<0 | elipse |
Para una fuerza repulsiva (α>0) la energía total E es siempre positiva por lo que solamente son posibles trayectorias hiperbólicas.
Cuando actúa además una perturbación
Consideremos ahora que sobre la partícula actúa además una perturbación inversamente proporcional al cubo de la distancia al centro de fuerzas.
donde (β>0) se refiere a una perturbación repulsiva y (β<0) se refiere a una perturbación atractiva. El potencial efectivo se escribirá ahora
Si L2+2mβ>0 la representación del potencial efectivo es similar a de las figuras que hemos visto anteriormente.
La ecuación de la trayectoria se obtiene integrando la ecuación diferencial (1), cuya solución es
Los valores de los parámetros d, ε y k son los siguientes
Periodos
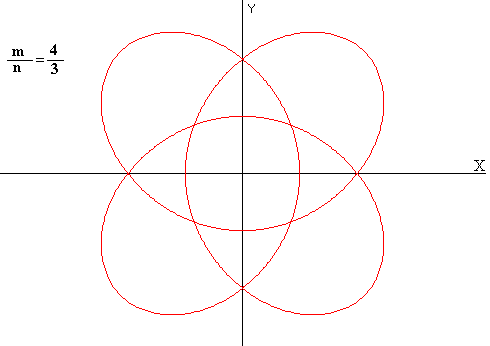
Fijándonos más específicamente en la figura, denominaremos periodo radial Pr al tiempo que tarda el móvil en dar dos pasos consecutivos por el perihelio o por el afelio, y el periodo orbital Pθ al tiempo necesario para que el móvil dé una vuelta completa al origen la relación entre ambos periodos es la siguiente
m Pr=n Pθ
Otro concepto interesante, es la velocidad de precesión Ω del afelio (perihelio), que se define como el cociente entre la distancia angular Δθ entre dos pasos consecutivos por el afelio (perihelio) y el tiempo que tarda o periodo radial Pr. La distancia angular es el intervalo para el cual kθ se incrementa en 2π es decir, Δθ=2π/k. La velocidad de precesión es
Calculemos ahora el periodo radial Pr en función de los parámetros de la trayectoria. De la ecuación de la constancia del momento angular
La ecuación de la trayectoria nos relaciona r y el ángulo θ. Integrando el segundo miembro
que nos da la relación entre el periodo radial Pr y los parámetros de la trayectoria d y ε
El periodo orbital y radial coinciden para un movimiento no perturbado (β=0) y por tanto, k=1. En este caso, el cuadrado del periodo es proporcional al cubo del semieje mayor de la elipse (tercera ley de Kepler).
Actividades
En el panel izquierdo del applet, están situados dos conjuntos de botones de radio correspondientes al grupo titulado Fuerza, y al grupo titulado Perturbación, para poder ensayar todas las combinaciones posibles: una fuerza atractiva o repulsiva combinada con una perturbación atractiva, repulsiva o nula.
En el control de edición titulado Excentricidad se introducirá un número decimal, mayor que la unidad si la fuerza es repulsiva, y mayor que cero y menor que uno, si la fuerza es atractiva.
Con el control de edición titulado Perturbación hay que tener más cuidado, ya que nos exige introducir un número decimal o una fracción irreductible dependiendo del caso. La etiqueta de dicho control cambia según la selección efectuada en los dos grupos de botones de radio.
Pulsando en el botón titulado Gráfica se representa la trayectoria.
Proporcionamos ejemplos de cada uno de los casos que se pueden producir
- Fuerza repulsiva (α>0), la energía E es positiva y el parámetro ε>1. Ejemplo ε=2
- Perturbación repulsiva (β>0) por lo que (k>1). La trayectoria es abierta. Ejemplo k=1.1
- Perturbación atractiva (β<0), por lo que (0<k<1). La partícula se mueve hacia el origen en una trayectoria en forma de espiral, para retornar de nuevo al infinito haciendo otra espiral. Ejemplo k=0.05
- Fuerza atractiva (α<0), la energía E puede ser positiva, negativa o nula.
- Si la energía E es positiva (E>0) el parámetro ε>1, la trayectoria es abierta, y los casos son análogos al de una fuerza repulsiva. Ejemplo ε=2
Si la perturbación es repulsiva, (β<0), son posibles varias trayectorias que pueden incidir sobre el origen, el numerador m del número racional que expresa k=m/n indica el número de tales trayectorias. Ejemplo k=4/1
Si la perturbación atractiva, (β<0), se obtienen trayectorias similares a la de la fuerza repulsiva, la partícula se mueve hacia el origen en forma de espiral. Aquí se puede introducir un número decimal o una fracción en el control de edición titulado Perturbación Ejemplo k=0.2, k=1/2.
- Si la energía total E es negativa (E<0) entonces el parámetro ε<1, la trayectoria está limitada y se presentan los casos más interesantes. Ejemplo ε=0.5
Cuando k se expresa como un número racional k=m/n el numerador m indica la simetría y el denominador n el número de vueltas que el radio vector da alrededor del origen. La órbita es cerrada siempre que k sea un número racional. Ejemplos k=6/1, k=7/6, k=1/3. Se introducirá siempre una fracción en el control de edición titulado Perturbación.
Referencias
Kotkin G. L., Serbo V. G-. Problemas de Mecánica Clásica. Editorial Mir (1980)
