Medida de la velocidad de la luz. Procedimiento de Roemer
La historia de la óptica es muy antigua, por ejemplo, se han encontrado espejos construidos en el antiguo Egipto.
No está claro quién inventó el primer telescopio, pero Galileo Galilei construyó su propio instrumento con el que descubrió el 7 de enero de 1610 los satélites de Júpiter. En dicho año observó los anillos de Saturno.
Pierre Fermat dedujo la ley de la refracción, a partir del principio del tiempo mínimo. La luz se propaga de un punto a otro a lo largo del camino que tarda un tiempo mínimo, aunque éste no sea el camino de menor longitud.
Hooke fue el primero en estudiar las interferencias generadas por películas delgadas. Propuso la idea de que la luz era un movimiento vibratorio rápido del medio propagándose a gran velocidad.
Newton permaneció ambivalente acerca de la naturaleza de la luz, aunque se inclinó finalmente por la teoría corpuscular.
Sin embargo, Huygens, se inclinó por la teoría ondulatoria, dedujo las leyes de la reflexión y de la refracción e incluso explicó la doble refracción de la calcita, usando a partir del modelo ondulatorio.
En aquella época, la luz era un chorro de partículas o una rápida ondulación de materia etérea. En cualquier caso, se estaba de acuerdo en que la velocidad de propagación era excesivamente grande. Roemer en 1676 midió la velocidad de la luz siguiendo el procedimiento que se detalla a continuación.
El procedimiento de Roemer
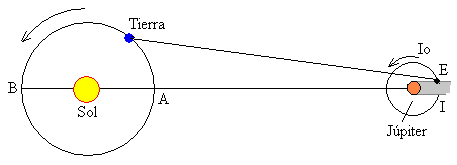
En la figura, se muestra el Sol, la Tierra, Júpiter y su satélite Io en su órbita alrededor de este planeta. El Sol ilumina Júpiter, que proyecta su sombra en el espacio.
Io es el satélite más cercano de Júpiter, y está situado prácticamente en el plano de su órbita alrededor del Sol. El satélite Io entra en la sombra proyectada por Júpiter por el punto I quedando oculto durante un pequeño intervalo de tiempo, y sale de la sombra por el punto E.
Durante medio año, el observador terrestre ve la aparición de Io oculto en la sombra de Júpiter, y durante el otro medio año la desaparición (eclipses) en dicha sombra.
Supongamos que la Tierra está en la posición A, la más cercana a Júpiter (oposición), cuando Io aparece de la sombra de Júpiter. El mismo acontecimiento ocurrirá 42.5 horas más tarde, cuando Io haya completado una vuelta.
La Tierra se mueve alrededor del Sol, después de N periodos de Io, la Tierra se encuentra en la posición B (conjunción) la más alejada de Júpiter.
Sea P' el periodo de Io medido por un observador terrestre y P el "verdadero" periodo de Io. La distancia entre la Tierra y Júpiter se ha incrementado en AB=d=2UA, el diámetro de la órbita aproximadamente circular de la Tierra alrededor del Sol
El astrónomo mide la diferencia NP'-NP=990 s, que será igual al cociente entre la distancia AB y la velocidad de la luz c.
Movimiento del sistema Sol-Tierra-Júpiter-Io
En el apartado anterior, se ha hecho una descripción simplificada del procedimiento de Roemer para medir la velocidad de la luz, en el que no se ha tenido en cuenta el movimiento de Júpiter, ni el cambio de orientación de la sombra proyectada. En este apartado haremos un estudio más detallado.
Para realizar los cálculos, supondremos que la Tierra, Júpiter describen órbitas circulares, ya que la excentricidad de la Tierra es 0.017 y la de Júpiter 0.048.
Los datos relativos a estos cuerpos celestes son los siguientes:
| Planeta | Radio de la órbita | Periodo |
| Tierra | 1.0 UA=1.496·1011 m | 365.26 días |
| Júpiter | 5.203 UA=7.78·1011 m | 11.86 años |
El radio ecuatorial de Júpiter es de rJ=71398 km=71.398·106 m
Ejercicio:
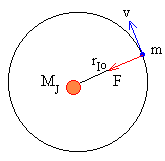 |
Io describe un órbita circular de radio rIo=4.216·108 m alrededor del planeta Júpiter, determinar su periodo. Datos: masa de Júpiter MJ=1.901·1027 kg, constante G=6.67·10-11 Nm2/kg2 |
Aplicamos la ecuación de la dinámica del movimiento circular uniforme
La velocidad orbital de Io es v=17342.2 m/s, y su periodo PIo=152748.4 s=42.4 h=1.768 días
| Satélite | Radio órbita m | Periodo |
| Io | 4.216·108 | 1.769 días |
Movimiento de la Tierra y Júpiter
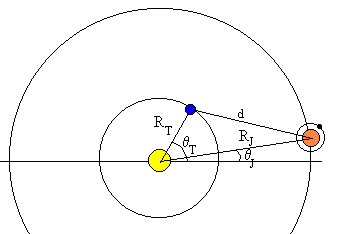
La Tierra y Júpiter se mueven en órbitas aproximadamente circulares alrededor del Sol.
- El radio de la órbita de la es RT=1.0 UA y su periodo PT=365.26 días.
- El radio de la órbita de Júpiter es RJ=5.203 UA y su periodo PJ=11.86 años.
Establecemos, un Sistema de Referencia con origen en el Sol.
- La posición de la Tierra en el instante t es (RT·cosθT, RT·sinθT)
- La posición de Júpiter en el instante t es (RJ·cosθJ, RJ·sinθJ)
La distancia d entre los centros de ambos planetas es
La mínima distancia, en el instante t=0, cuando θT=θJ=0 es RJ-RT=5.203-1.0=4.203 UA
La distancia entre la Tierra y Júpiter va aumentando, medio año después la Tierra se encuentra en la posición θT=π. Júpiter debido a su menor velocidad angular, se encuentra en θJ=2·π·½ año/11.86 años=π/11.86=0.264 rad=15.2º
La distancia entre la Tierra y Júpiter en dicho instante es d=6.174 UA. Un poco menor que la distancia entre la Tierra y Júpiter suponiendo que éste permanece en reposo d=5.203+1.0=6.203 UA.
En una primera aproximación, podemos suponer que Júpiter permanece en reposo en la posición θJ≈0 durante el medio año que duran las observaciones de su satélite Io.
Movimiento de Io
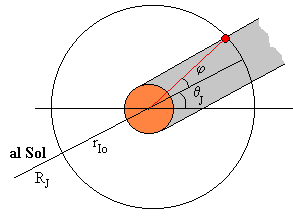 El satélite Io describe
una órbita circular de radio rIo=4.216·108 m situada en el plano de la órbita de Júpiter alrededor del Sol.
El Sol ilumina Júpiter que proyecta su sombra en el espacio. La anchura de la sombra es igual al diámetro de Júpiter, cuyo radio es de
71398 km.
El satélite Io describe
una órbita circular de radio rIo=4.216·108 m situada en el plano de la órbita de Júpiter alrededor del Sol.
El Sol ilumina Júpiter que proyecta su sombra en el espacio. La anchura de la sombra es igual al diámetro de Júpiter, cuyo radio es de
71398 km.
El desplazamiento angular φ de Io en la sombra del planeta Júpiter es
Sabiendo que la velocidad angular de Io es el cociente entre 2π (una vuelta) y el periodo de revolución PIo=1.769 días, el tiempo que Io permanece en la sombra del planeta Júpiter es
A medida que se mueve el planeta Júpiter su sombra va cambiando de orientación un ángulo θ J igual al que forma el radio vector que une el Sol con el planeta y la horizontal, tal como puede verse en la figura.
Io no aparece y desaparece de forma instantánea en la sombra proyectada por Júpiter, como su radio ecuatorial es de 1820 km, por tanto, el tiempo que tarda en aparecer y desaparecer es igual al cociente entre el diámetro y la velocidad orbital vIo=17342.2 m/s calculada en el ejercicio anterior. El resultado es 3.5 minutos.
El radio de la órbita de Io rIo=4.216·108 m es muy pequeño en comparación incluso con la distancia mínima entre la Tierra y Júpiter 4.203·1.496·1011 =6.29·1011 m, por lo que la distancia entre Io (en el momento en el que aparece de la sombra de Júpiter) y la Tierra es aproximadamente igual a la distancia entre Júpiter y la Tierra.
Incremento del periodo observado de Io
El periodo de Júpiter es de 11.86 años, durante el medio año en el que van a realizarse las observaciones de su satélite Io, su posición cambia muy poco. Supondremos también, que el radio de Io es muy pequeño comparado con la distancia entre Júpiter y la Tierra
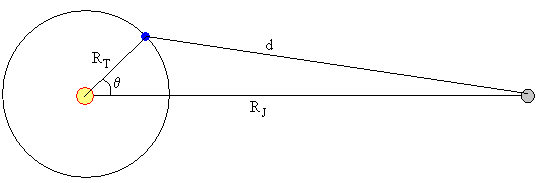
Cuando la Tierra está en la posición más cercana a Júpiter la distancia entre estos dos planetas es 5.203-1.0=4.203 UA. Cuando la Tierra está en la posición más alejada de Júpiter la distancia entre estos dos planetas es 5.203+1.0=6.203 UA.
Cuando la Tierra forma un ángulo θ con la recta que une Júpiter y el Sol, la distancia d es
Como la velocidad angular de la Tierra ωT =2π/365.26 rad/día, su posición es θ=ωT·t
Supongamos que cuando la Tierra está en la posición más cercana a Júpiter, θ=0, a una distancia d1=4.203 UA, ve salir por primera vez a Io de la sombra de Júpiter. Un periodo de Io después P=1.769 días, la Tierra se encuentra en la posición θ=ωT·P=0.03 rad=1.74º. La distancia entre la Tierra y Júpiter es d2=4.2036 UA
La diferencia de tiempo entre dos apariciones consecutivas de Io debida al incremento de distancia d2-d1 entre Júpiter y la Tierra es
Donde c es la velocidad de la luz c=3.0·108 m/s. En este caso Δt=0.286 s,
Comparemos dos observaciones consecutivas de la aparición de Io.
En la observación i, el ángulo que forma la Tierra con la recta que une el Sol y Júpiter es θ=i·ωT·P, la distancia entre la Tierra y Júpiter es
En la observación i+1, el ángulo que forma la Tierra con la recta que une el Sol y Júpiter es θ=(i+1)·ωT·P, la distancia entre la Tierra y Júpiter es
La diferencia de tiempo entre dos apariciones consecutivas de Io debida al incremento de distancia di+1-di entre Júpiter y la Tierra es
En medio año, el número total de observaciones es (365.26/2)/1.796=102
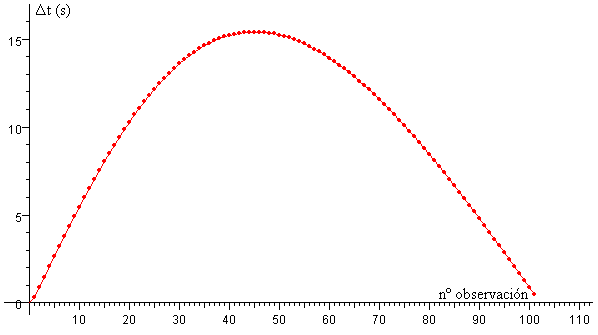
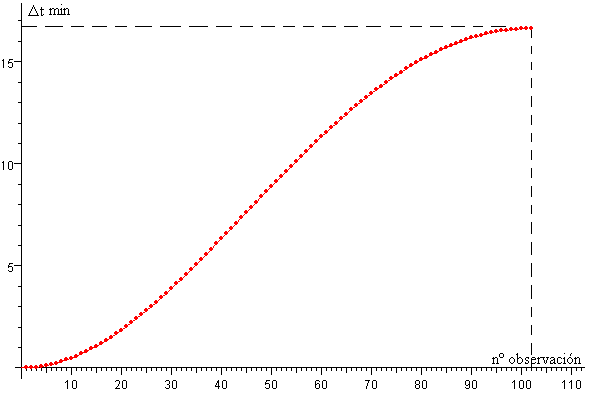
En la figura, se representa Δt en segundos en función del número de observación. Si la Tierra parte de la posición θ=0 (oposición), la figura nos muestra que los periodos observados de Io se van incrementando a medida que la Tierra se aleja de Júpiter hasta que alcanza la cuadratura θ=90º. Después, van disminuyendo hasta que se alcanza la conjunción θ=180º
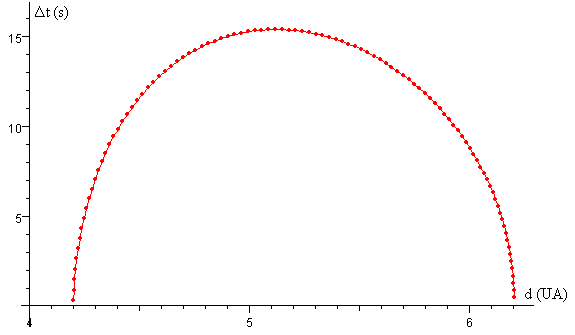
En la figura, se representa el incremento del periodo observado de Io Δt en función de la distancia (en UA) entre la Tierra y Júpiter
Velocidad relativa de la Tierra respecto de Júpiter
La velocidad relativa de la Tierra respecto a Júpiter se calcula proyectando los vector velocidad de ambos planetas, cuya dirección es perpendicular al radio de su órbita, a lo largo de la recta que une ambos planetas.
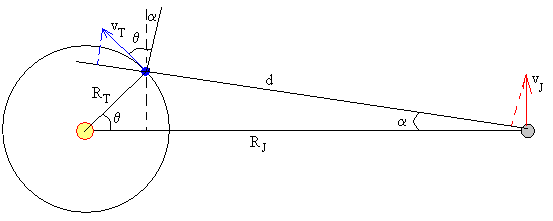
Como vemos en la figura la velocidad relativa vr vale
vr=vT·sin(α+θ)-vJ·senα
Como la Tierra tarda 365.26 días en dar una vuelta completa. La velocidad de la Tierra es
Como Júpiter tarda 11.86 años en dar una vuelta completa. La velocidad de Júpiter es
Conocido el ángulo θ calculamos el ángulo α.
En esta otra figura, se representa el incremento del periodo observado de Io, Δt en función de la velocidad relativa entre la Tierra y Júpiter a lo largo de la línea que une ambos planetas. Este incremento Δt es proporcional a la velocidad relativa vr entre la Tierra y Júpiter. Se trata por tanto, de un efecto Doppler.
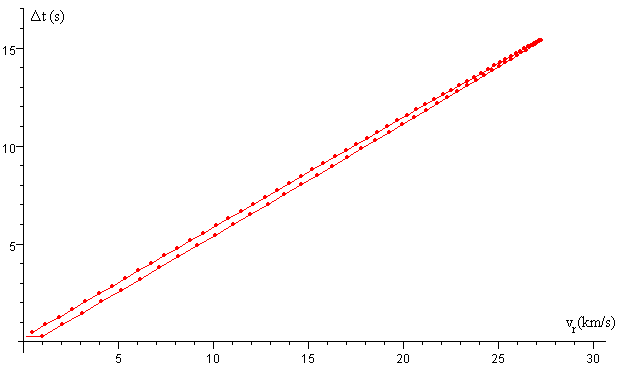
Cada aparición de Io de la sombra de Júpiter representa una señal luminosa periódica que se repite cada 1.796 días emitida por un observador en movimiento. La señal luminosa viaja por el espacio a la velocidad de la luz y es vista por un observador terrestre en movimiento. El periodo P' de la señal recibida y el periodo P de la señal emitida están relacionadas por la fórmula que describe el efecto Doppler.
Retraso de las apariciones de Io
Es muy difícil medir una diferencia de tiempo menor que 15 segundos ente dos observaciones consecutivas de la aparición de Io. Sin embargo, es posible medir el retraso de la última observación medio año después.
La primera observación tiene lugar cuando la Tierra está más cercana a Júpiter d1=5.203-1.0=4.203 UA;
Como el periodo de Io es de P=1.796 días. La observación i de la aparición de Io de la sombra de Júpiter cabría esperar que tuviese lugar en el instante t=i·P. Debido a que la Tierra se aleja de Júpiter, la observación i tiene lugar en el instante t'=iP+Δt. Donde el retraso Δt vale
Por ejemplo para la última observación i=102, el ángulo θ=i·ωT·P≈π=180º, que forma la Tierra con la recta que une el Sol y Júpiter, Δt=997 s=16.6 min
Actividades
En el applet observamos, en la parte superior el movimiento de la Tierra y de Júpiter a lo largo de medio año.
En la parte inferior, observamos el movimiento del satélite Io, visto con un "telescopio".
Cada vez que Io reaparece después de haber estado oculto por la sombra de Júpiter el "astrónomo" apunta el número de observación y el momento de dicha observación (en días, horas y minutos). La primera observación marca el tiempo inicial cero. También anota las posiciones angulares de la Tierra y de Júpiter medidas en grados.
En la simulación, se tiene en cuenta el movimiento de Júpiter a lo largo de medio año, y que las órbitas que describe la Tierra y Júpiter son elípticas.
En la parte inferior izquierda, se representa el tiempo de retraso de la aparición de Io. Este retraso es de unos 1000 segundos, para la última observación, cuando la Tierra se encuentra en la posición más alejada de Júpiter.
Para obtener el valor de la velocidad de la luz, Roemer supuso que la causa del retraso era el incremento de la distancia entre la Tierra y Júpiter y que Júpiter se mueve relativamente poco durante el periodo de medio año terrestre, por lo que la luz recorre aproximadamente una distancia extra igual al diámetro de la órbita terrestre 2 UA. La velocidad de la luz será, entonces
Referencias
Shea J. H., Ole Rǿmer, the speed of light, the apparent period of Io, the Doppler effect, and the dynamics of Earth and Jupiter. Am. J. Phys. 66 (7) July 1988, pp. 561-569
