El átomo de Bohr
 En el capítulo Electromagnetismo se estudia el modelo de átomo de Bohr como ejemplo de movimiento de una carga (el
electrón) bajo la fuerza de atracción del núcleo.
En el capítulo Electromagnetismo se estudia el modelo de átomo de Bohr como ejemplo de movimiento de una carga (el
electrón) bajo la fuerza de atracción del núcleo.
Supongamos que un electrón describe una órbita circular de radio r
Para que la órbita corresponda a un estado estacionario, la longitud de la circunferencia de radio r deberá ser un múltiplo entero de la longitud de onda λ tal como se ve en la figura.
2πr=nλ
La longitud de onda de de Broglie de una partícula de masa me que se mueve con velocidad v es onda λ=h/p. Donde h es la constante de Planck, y p=mev es el momento lineal del electrón.
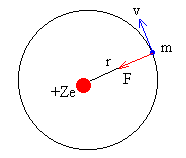 La dinámica del movimiento circular uniforme nos dice
que la fuerza de atracción entre el núcleo de carga +Ze y el electrón e es igual al producto de la masa del electrón por la aceleración
normal
La dinámica del movimiento circular uniforme nos dice
que la fuerza de atracción entre el núcleo de carga +Ze y el electrón e es igual al producto de la masa del electrón por la aceleración
normal
Eliminando v en estas dos ecuaciones obtenemos el radio de las órbitas permitidas del electrón del átomo de Hidrógeno o ión hidrogenoide.
donde a0 se denomina radio de Bohr. a0 es el radio de la órbita del electrón del átomo de Hidrógeno Z=1 en su estado fundamental n=1
La energía del electrón en una órbita circular de radio r vale
En una órbita circular la energía total E es la mitad de la energía potencial
La energía del electrón aumenta con el número cuántico n.
Actividades
Se introduce
-
El número cuántico n, del electrón en el átomo de Hidrógeno Z=1,
Se pulsa el botón titulado Gráfica
Para el valor de n seleccionado, se representa la órbita circular de radio r, y la onda estacionaria de de Broglie de longitud de onda λ, tal que 2πr=nλ.
Referencias
Blomm D., Blomm D. W. Vibrating wire loop and the Bohr model. The Physics Teacher, 41, May 2003, pp. 292-294
