Termodinámica de un choque inelástico
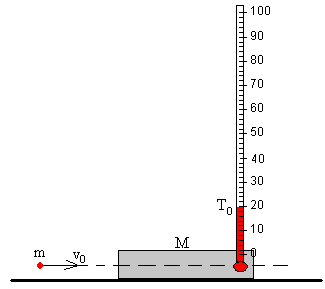
En esta página estudiamos un sistema aislado formado por una bala y un bloque de forma rectangular. La bala se dispara horizontalmente contra una de las caras del bloque a lo largo de la línea que pasa por su centro de masas, penetra en el bloque una cierta distancia hasta que ambos adquieren la misma velocidad.
El bloque está inicialmente en reposo mientras que la bala tiene una velocidad inicial v0. El bloque y la bala están inicialmente a la temperatura T0 y ambos tienen una conductividad tan alta que alcanzan en cada instante una temperatura común T.
El bloque y la bala forman un sistema aislado de modo que despreciaremos la resistencia del aire, pérdidas térmicas o de radiación con el exterior.
Descripción en el sistema de referencia del centro de masas
Dado que el sistema formado por la bala y el bloque es aislado, el momento lineal total o la velocidad de su centro de masas vcm permanece constante.
En el sistema de referencia del centro de masas, la velocidad inicial de la bala es
La velocidad inicial del bloque es
La velocidad final del bloque y la bala es cero.
La variación de energía cinética del sistema formado por la bala y el bloque en el sistema de referencia del centro de masas es
El sistema pierde energía mecánica que se transforma en energía interna ya que el sistema es aislado
Como consecuencia la temperatura de la bala y del bloque se elevan.
ΔU=(mc1+M·c2)(Tf-T0)
c1 y c2 son los calores específicos de la bala y el bloque, respectivamente. T0 es la temperatura inicial.
Tf es la temperatura final
El cambio de entropía del sistema aislado es
El proceso es irreversible por lo que ΔS>0
Fuerza interna constante.
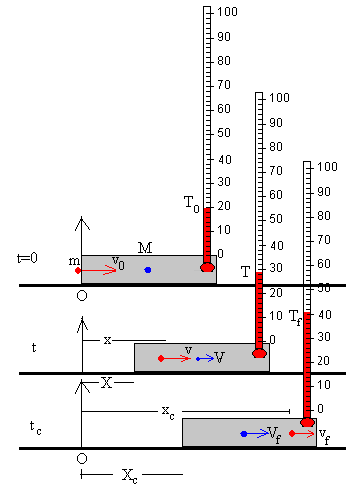
En este apartado repetiremos la descripción dada en la página titulada “Choque inelástico de duración finita”
A medida que la bala penetra en el bloque, la bala ejerce una fuerza F que supondremos constante sobre el bloque y su efecto será el de incrementar su velocidad.
A su vez, el bloque ejercerá una fuerza F igual y opuesta sobre la bala cuyo efecto será el de disminuir su velocidad. El choque se completará cuando la velocidad de la bala se iguale a la del bloque.
Tenemos así que estudiar la dinámica de un sistema aislado formado por dos partículas que interaccionan entre sí. La interacción se describe en términos de una fuerza constante F.
Velocidades antes y después del choque
Cuando la bala penetra, la fuerza constante F que ejerce el bloque hace que disminuya su velocidad.
v=v0-F·t/m
La fuerza F igual y de sentido contrario que ejerce la bala sobre el bloque hace que éste incremente su velocidad
V= F·t/M
El choque finaliza cuando la velocidad v de la bala se iguala a la velocidad V del bloque, es decir en el instante tc, medido desde el momento en el que la bala penetra en el bloque.
La velocidad final del bloque Vf y de la bala vf en dicho instante es
que es a su vez la velocidad del centro de masas del sistema aislado y es independiente del valor de la fuerza F.
Desplazamientos de la bala y del bloque
Si la bala y la cara anterior del bloque están en el origen en el momento en el que la bala entra en contacto con el bloque, al cabo de un cierto tiempo t<tc, la posición de la bala x y la posición del bloque X serán, respectivamente
En el instante tc en el que finaliza el choque, la bala habrá penetrado una distancia xc-Xc en el interior del bloque. El trabajo realizado por la fuerza F será
El signo menos se debe a que la fuerza F sobre la bala es de sentido contrario a su desplazamiento
La fuerza interior F realiza un trabajo que modifica la energía cinética de las partículas del sistema.
Temperatura del sistema formado por el bloque y la bala
El trabajo de la fuerza interna F se transforma en energía interna del sistema aislado, como consecuencia se eleva la temperatura del bloque y de la bala.
ΔU=|W|=(mc1+M·c2)(T-T0)
La temperatura final Tf será
La bala atraviesa el bloque
Cuando la bala atraviesa el bloque la fuerza interior F realiza un trabajo W=-F·L
Siendo L la longitud del bloque. La temperatura final será, en este caso
Ejemplo:
- Masa de la bala, m=0.4 kg
- Velocidad de la bala, v0=10 m/s
- Fuerza de interacción, F=20 N
- La masa del bloque, M=1kg
- El calor específico de la bala y del bloque, c1=c2=0.5 J/(kg·K)
- La temperatura inicial, T0=20ºC
La bala y el bloque alcanzan la misma velocidad en el instante tc
Los desplazamientos de la bala y el bloque son
La bala ha penetrado en el bloque una distancia
d=xc-Xc=0.71 m
La velocidad final del conjunto bala-bloque una vez completado el choque es
Conocidas las velocidades iniciales y finales de las partículas calculamos la variación de energía cinética
ΔE=-14.3 J
que tiene el mismo valor que el trabajo realizado por la fuerza de interacción F
W=-F(xc-Xc)
Temperatura final es
Actividades
Se introduce
- La masa m de la bala en kg, en el control de edición titulado Masa bala
- La velocidad v0 de la bala en m/s, en el control de edición titulado Velocidad bala
- La fuerza F en N de interacción entre le bloque y la bala, moviendo el dedo en la barra de desplazamiento titulado Fuerza.
- La masa del bloque se ha fijado en M=1kg
- La longitud del bloque se ha fijado en el valor L=1 m
- El calor específico de la bala y del bloque se ha fijado en c1=c2=0.5 J/(kg·K)
- La temperatura inicial se ha fijado en T0=20ºC
Se pulsa el botón titulado Empieza
Se observa el movimiento de la bala, cómo va penetrando en el bloque a la vez que disminuye su velocidad y aumenta la del bloque.
En la parte izquierda del applet, observamos los cambios energéticos:
- la energía cinética del bloque en color azul
- la energía cinética de la bala en color rojo
- el trabajo de la fuerza de interacción F en color gris, que como vemos disminuye la energía cinética del sistema de partículas.
En la parte derecha,
- La temperatura del sistema aislado formado por el bloque y la bala
Referencias
Mungan C. E. Thermodynamics of a block sliding across a frictional surface. The Physics Teacher Vol 45, May 2007, pp. 288-291
