Aproximación al equilibrio de dos gases contenidos en un recinto adiabático y separados por un émbolo (I)
En esta página, se estudia la evolución hacia el estado de equilibrio de un sistema aislado formado por dos gases ideales contenidos en un cilindro de sección S separados por una pared adiabática. Inicialmente el émbolo está fijo. Las características de los dos gases son las siguientes:
- El primer gas ocupa un volumen V10 y el segundo V20
- El número de moles son n1 y n2, respectivamente
- Las presiones iniciales de los dos gases en sus recipientes son p10 y p20
- Las temperaturas iniciales son T10 y T20 tal que
R=8.3143 J/(K·mol) es la constante de los gases
- Se puede elegir que los gases puedan ser monoatómicos o diatómicos, sus calores específicos a volumen constante cv, a presión constante cp y el índice adiabático γ son, respectivamente
En el instante t=0, se libera el émbolo. El sistema alcanzará el equilibrio cuando las presiones de los gases separados por el émbolo en reposo sean las mismas p1f=p2f=pf
- Aplicamos la ecuación de los gases ideales a cada una de las partes
- Como el sistema es aislado, la energía total permanece constante
- Los volúmenes de los gases cambian, pero el volumen total es constante e igual al inicial que ocupaban los gases.
pf·V1f=n1RT1f
pf·V2f=n2RT2f
U1f+U2f=U10+U20
La energía interna de un gas ideal solamente depende de la temperatura
n1cv1T1f+n2cv2T2f= n1cv1T10+n2cv2T20
V10+V20=V1f+V2f
Ahora bien, de estas ecuaciones no podemos despejar los volúmenes finales ni las temperaturas finales. Es preciso hacer ciertas hipótesis acerca del movimiento del émbolo y su interacción con las moléculas del gas. En esta página, se describe el movimiento del émbolo en base a un modelo simple. En la siguiente página, se describe en términos de los choques de las moléculas de un gas ideal con una pared móvil.
Movimiento del émbolo
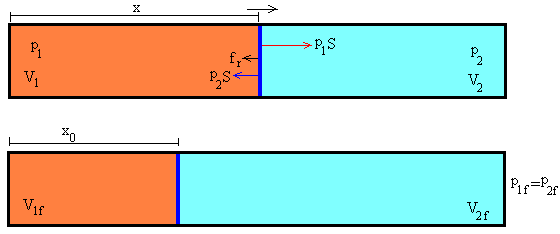
El émbolo de masa m se mueve cuando hay una la diferencia de presión entre los dos gases que separa.
(p1-p2)S
Supondremos además, que el émbolo experimenta una fuerza de rozamiento proporcional a su velocidad y de sentido contrario a ésta.
donde e es una constante de proporcionalidad y x’=x-x0 es la posición del émbolo respecto de la posición de equilibrio x0. Cuando se alcanza el estado de equilibrio el volumen final del gas 1 es V1f.
La ecuación del movimiento del émbolo se escribe
Donde hemos empleado la ecuación de la transformación adiabática
Hemos obtenido la ecuación diferencial que nos da el volumen V1 del gas 1 en función del tiempo.
k1 y k2 serían constantes si no se tuviese en cuenta el rozamiento, pero no pueden serlo si lo hay como vamos a ver a continuación.
Trabajo de la fuerza de rozamiento
El trabajo realizado por la fuerza de rozamiento se transforma en calor que se reparte entre los dos recipientes. En el tiempo dt se genera el calor
Una fracción α de este calor se transfiere al gas 1 y el resto, (1-α) al gas 2.
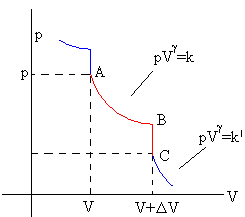
Vamos ahora a estudiar el proceso por el cual el gas en el intervalo de tiempo Δt, cambia su volumen de V a V+ΔV. Este proceso lo podemos dividir por conveniencia en dos etapas:
- Etapa A→B, adiabática, el gas produce trabajo
- Etapa B→C, isócora, el gas absorbe calor
En la transformación adiabática A→B
donde k es la constante que caracteriza el proceso adiabático
En la transformación isócora B→C,
El trabajo de la fuerza de rozamiento se transforma en calor, una parte del cual se transfiere al gas, que incrementa su energía interna, es decir su temperatura.
Al finalizar el proceso la nueva constante k’ que caracteriza la etapa adiabática del siguiente proceso que comienza en el instante t+Δt valdrá
Vamos a relacionar k’ con k teniendo en cuenta que ΔV<<V
En el límite, cuando el intervalo de tiempo Δt→0
Sistema de ecuaciones diferenciales
El comportamiento del sistema formado por los dos gases y el émbolo de acuerdo con el modelo adoptado, se describe por el siguiente sistema de ecuaciones diferenciales:
Resolvemos el sistema de ecuaciones diferenciales por procedimientos numéricos, con las siguientes condiciones iniciales.
En el instante t=0.
Como el sistema formado por los dos gases y el émbolo es aislado la energía total permanecerá constante e igual a la inicial.
donde v=dx’/dt es la velocidad del émbolo
La constancia de la energía del sistema en cada instante es el criterio que nos permitirá probar la adecuación del procedimiento numérico para la resolución del sistema de ecuaciones diferenciales.
Ejemplos
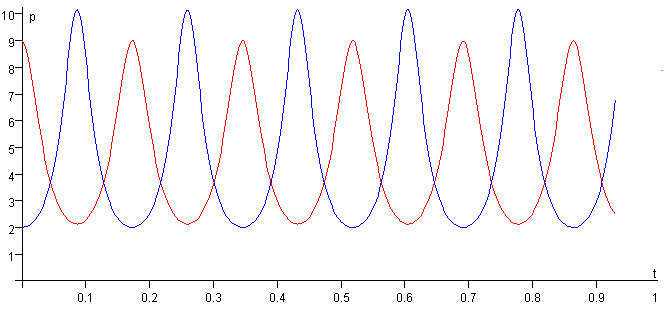
Si no hay rozamiento. El émbolo oscila permanentemente, no se alcanza el estado de equilibrio.
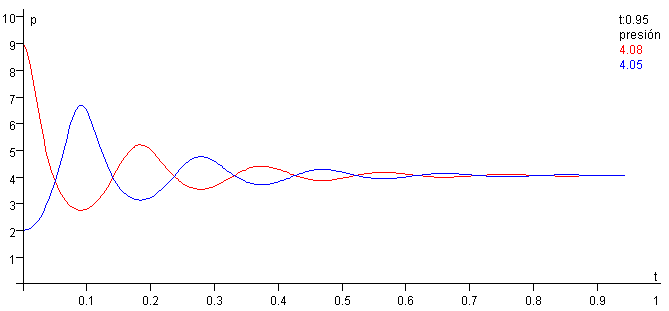
Si hay rozamiento, el émbolo describe una especie de oscilación amortiguada, al cabo de un cierto tiempo se alcanza el equilibrio igualándose las presiones de los dos gases a ambos lados del émbolo.
Actividades
Se introduce
- Para cada uno de los dos gases:
- La presión, en unidades 105 Pa, en los dos controles de edición titulados Presión
- El volumen, en litros, 10-3 m3, en los dos controles de edición titulados Volumen
- El número de moles, en los dos controles de edición titulados n. moles
- Se activa el botón de radio titulado M (monoatómico) o D (diatómico) en Tipo de gas
- El coeficiente e de proporcionalidad de la fuerza de rozamiento, en el control de edición titulado Rozamiento
- La masa m del émbolo en kg, en el control de edición titulado Masa
- El área del émbolo se ha fijado en S=2.0·10-4 m2
- El calor producido por el émbolo al desplazarse se reparte por igual entre los dos gases α=0.5.
Se pulsa el botón titulado Inicio
Se pueden seleccionar cuatro modos de visualización:
- El dispositivo: El sistema formado por los dos gases separados por un émbolo móvil. Los termómetros nos señalan la temperatura de cada gas en kelvin. Un diagrama en forma de tarta en la parte superior del applet, nos muestra las transformaciones energéticas:
- En color rojo, la energía del gas situado a la izquierda del applet
- En color azul, la energía del gas situado a la derecha
- En color gris, la energía cinética del émbolo.
- Gráfica P-t: se muestra la gráfica de la presión (eje vertical) en función del tiempo (eje horizontal). La presión está en unidades de 105 Pa
- Gráfica V-t: se muestra la gráfica del volumen (eje vertical) en función del tiempo (eje horizontal). El volumen está en litros (10-3 m3)
- Gráfica T-t: se muestra la gráfica de la temperatura (eje vertical) en función del tiempo (eje horizontal).
Se pulsa el botón titulado Empieza
Referencias
Anacleto J., Anacleto J. A. C. Thermodynamical interactions: subtleties of heat and work concepts. Eur. J. Phys. 29 (2008) 555-566
