Los métodos de Montecarlo
Los métodos de Montecarlo abarcan una colección de técnicas que permiten obtener soluciones de problemas matemáticos o físicos por medio de pruebas aleatorias repetidas. En la práctica, las pruebas aleatorias se sustituyen por resultados de ciertos cálculos realizados con números aleatorios. Se estudiará el concepto de variable aleatoria y la transformación de una variable aleatoria discreta o continua.
Ejemplos sencillos son: el mecanismo básico de la dfusión y el establecimiento del equilibrio térmico entre dos sistemas que se ponen en contacto a distinta temperatura. Estos dos ejemplos nos mostrarán el significado de proceso irreversible y fluctuación alrededor del estado de equilibrio.
La explicación de la ley exponencial decreciente en la desintegración de una sustancia radioactiva en otra estable. Comprender, a partir de un modelo simple de núcleo radioactivo, que su desintegración es un suceso aleatorio, con mayor o menor probabilidad dependiendo de la anchura de las barreras de potencial que mantienen confinadas a las partículas que componen el núcleo.
Otros ejemplos relevantes son: el estudio de un sistema con un número pequeño de estados como paso previo al estudio del comportamiento de un material paramagnético bajo la ación de un campo magnético y a una determinada temperatura, dos ejemplos de aplicación de la transformación de una variable discreta. Por último, estudiaremos el comportamiento de un material dieléctrico como ejemplo de aplicación de transformación de una variable aletoria continua.
La variable aleatoria
Se denomina variable aleatoria, a una variable X que puede tomar un conjunto de valores {x0, x1, x2, ... xn-1}, con probabilidades {p0, p1, p2, ... pn-1}. Por ejemplo, en la experiencia de lanzar monedas, los posibles resultados son {cara, cruz}, y sus probabilidades son {1/2, 1/2}. En la experiencia de lanzar dados, los resultados posibles son {1, 2, 3, 4, 5, 6} y sus probabilidades respectivas son {1/6, 1/6, 1/6, 1/6, 1/6, 1/6}.
Realicemos ahora la experiencia de hacer girar una ruleta y apuntar el número del sector que coincide con la flecha. En la ruleta de la izquierda de la figura los resultados posibles son {0, 1, 2, 3, 4, 5, 6, 7}, y la probabilidad de cada resultado es 1/8. En la ruleta de la derecha de la figura los posibles resultados son {0, 1, 2, 3}, y las probabilidades respectivas {1/4, 1/2, 1/8, 1/8}, proporcionales al ángulo del sector.
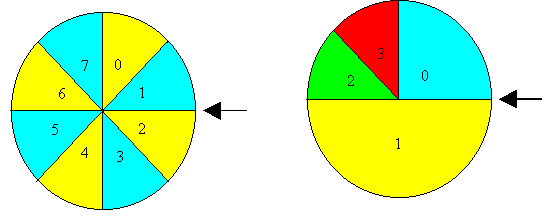
En los tres primeros ejemplos, la variable aleatoria X se dice que está uniformemente distribuida, ya que todos los resultados tienen la misma probabilidad. Sin embargo, en el último ejemplo, la variable aleatoria X, no está uniformemente distribuida.
El problema crucial de la aplicación de los métodos de Montecarlo es hallar los valores de una variable aleatoria (discreta o continua) con una distribución de probabilidad dada por la función p(x) a partir de los valores de una variable aleatoria uniformemente distribuida en el intervalo [0, 1), proporcionada por el ordenador o por una rutina incorporada al programa.
Para simular un proceso físico, o hallar la solución de un problema matemático es necesario usar gran cantidad de números aleatorios. El método mecánico de la ruleta sería muy lento, además cualquier aparato físico real genera variables aleatorias cuyas distribuciones difieren, al menos ligeramente de la distribución uniforme ideal. También, se puede hacer uso de tablas de cifras aleatorias uniformemente distribuidas, comprobadas minuciosamente en base a pruebas estadísticas especiales. Se emplean solamente cuando los cálculos correspondientes a la aplicación del método de Montecarlo se realiza a mano, lo que en estos tiempos resulta inimaginable. En la práctica, resulta más conveniente emplear los denominados números pseudoaleatorios, se trata de números que se obtienen a partir de un número denominado semilla, y la aplicación reiterada de una fórmula, obteniéndose una secuencia {x0, x1, x2, ... xn} de números que imitan los valores de una variable uniformemente distribuida en el intervalo [0, 1).
Variable aleatoria discreta
Para simular la ruleta situada a la derecha de la figura, se procede del siguiente modo: se hallan las probabilidades de cada resultado, proporcionales al ángulo de cada sector y se apuntan en la segunda columna, la suma total debe de dar la unidad. En la tercera columna, se escriben las probabilidades acumuladas.
| Resultado | Probabilidad | P. acumulada |
| 0 | 0.25 | 0.25 |
| 1 | 0.5 | 0.75 |
| 2 | 0.125 | 0.875 |
| 3 | 0.125 | 1 |
Se sortea un número aleatorio γ uniformemente distribuido en el intervalo [0, 1), el resultado del sorteo se muestra en la figura. En el eje X se sitúan los distintos resultados que hemos nombrado x0, x1, x2, x3 . En el eje vertical las probabilidades en forma de segmentos verticales de longitud igual a la probabilidad pi de cada uno de los resultados, dichos segmentos se ponen unos a continuación de los otros, encima su respectivo resultado xi. Se obtiene así una función escalonada. Cuando se sortea una variable aleatoria γ, se traza una recta horizontal cuya ordenada sea γ. Se busca el resultado cuya abscisa sea la intersección de dicha recta horizontal y del segmento vertical, tal como se señala con flechas en la figura. Si el número aleatorio γ está comprendido entre 0.25 y 0.75 se obtiene el resultado denominado x1.
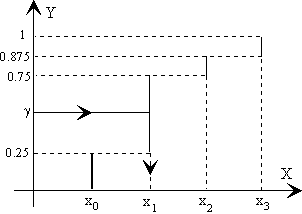
La tabla describe el sorteo de una variable discreta, siendo γ una variable aleatoria uniformenente distribuída en el intervalo [0,1).
| Condición | Resultado |
| 0<=γ<0.25 | 0 |
| 0.25<=γ<0.75 | 1 |
| 0.75<=γ<0.875 | 2 |
| 0.875<=γ<1 | 3 |
Una vez visto un caso particular, el problema general puede formularse del siguiente modo:
Si X es una variable aleatoria discreta cuyos posible resultados son {x0, x1, x2 , ... xn-1} y sean {p0, p1, p2, ... pn} sus respectivas probabilidades. Al sortear un número aleatorio γ, uniformemente distribuido en el intervalo [0, 1), se obtiene el resultado xi, si se verifica la siguiente condición
Variable aleatoria continua
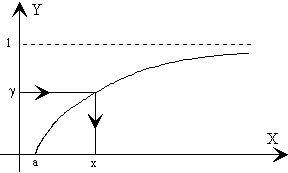
Comprendido el concepto de transformación de una variable discreta, y el procedimiento para obtener un resultado cuando se efectúa el sorteo de una variable aleatoria uniformemente distribuida, no reviste dificultad el estudio de la variable continua. Si X es una variable aleatoria continua, y p(x) es la probabilidad de cada resultado x, construimos la función que se representa en la figura.
El resultado del sorteo de una variable γ uniformemente distribuida en el intervalo [0 ,1) se obtiene a partir de la ecuación.
Gráficamente, se obtiene trazando una recta horizontal de ordenada γ. La abscisa x del punto de corte con la función es el resultado obtenido. En la figura se señala mediante flechas.
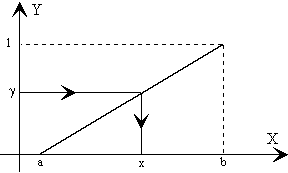
Un ejemplo sencillo es la transformación de una variable aleatoria que está uniformemente distribuida en el intervalo [a, b) si
Integrando (2) obtenemos la función
que es una línea recta, que vale cero cuando x=a, y uno cuando x=b, tal como puede verse en la figura inferior. Utilizando la fórmula (3) de la transformación de la variable aleatoria continua y despejando x, se obtiene
Generador de números aleatorios
Existen varias fórmulas para obtener una secuencia de números aleatorios, una de las más sencillas es la denominada fórmula de congruencia: se trata de una fórmula iterativa, en la que el resultado de una iteración se utiliza en la siguiente.
x=(a*x+c)%m;
donde a, c, m, son constantes cuyos valores elige el creador de la rutina, así por ejemplo tenemos
a=24298 c=99491 m=199017
a=899 c=0 m=32768
Basta introducir el valor inicial de x, para obtener una secuencia de números pseudoaleatorios. Alternativamente, podemos usar la clase Random que dispone el lenguaje Java.
Bibliografía
I. M. Sóbol. Métodos de Montecarlo. Lecciones populares de Matemáticas. Editorial Mir (1976).
B. P. Demidowitsch. I. A. Maron, E. S. Schuwalowa. Métodos numéricos de análisis. Editorial Paraninfo (1980).
