Regresión lineal
Abordaremos en esta página las distribuciones bidimensionales. Las observaciones se dispondrán en dos columnas, de modo que en cada fila figuren la abscisa x y su correspondiente ordenada y. La importancia de las distribuciones bidimensionales radica en investigar como influye una variable sobre la otra. Esta puede ser una dependencia causa efecto, por ejemplo, la cantidad de lluvia (causa), da lugar a un aumento de la producción agrícola (efecto). O bien, el aumento del precio de un bien, da lugar a una disminución de la cantidad demandada del mismo.
Si utilizamos un sistema de coordenadas cartesianas para representar la distribución bidimensional, obtendremos un conjunto de puntos conocido con el diagrama de dispersión, cuyo análisis permite estudiar cualitativamente, la relación entre ambas variables tal como se ve en la figura. El siguiente paso, es la determinación de la dependencia funcional entre las dos variables x e y que mejor ajusta a la distribución bidimensional. Se denomina regresión lineal cuando la función es lineal, es decir, requiere la determinación de dos parámetros: la pendiente y la ordenada en el origen de la recta de regresión, y=ax+b.
La regresión nos permite además, determinar el grado de dependencia de las series de valores X e Y, prediciendo el valor y estimado que se obtendría para un valor x que no esté en la distribución.
Varias páginas del Curso Interactivo de Física describen ejemplos de aplicación de la Regresión lineal.
Descripción
Vamos a determinar la ecuación de la recta que mejor ajusta a los datos representados en la figura. Se denomina error ei a la diferencia yi-y, entre el valor observado yi, y el valor ajustado y= axi+b, tal como se ve en la figura inferior. El criterio de ajuste se toma como aquél en el que la desviación cuadrática media sea mínima, es decir, debe de ser mínima la suma
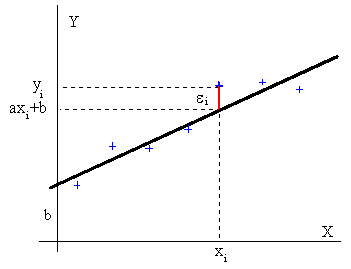
El extremos de una función: máximo o mínimo se obtiene cuando las derivadas de s respecto de a y de b sean nulas. Lo que da lugar a un sistema de dos ecuaciones con dos incógnitas del que se despeja a y b.
El coeficiente de correlación es otra técnica de estudiar la distribución bidimensional, que nos indica la intensidad o grado de dependencia entre las variables X e Y. El coeficiente de correlación r es un número que se obtiene mediante la fórmula.
El numerador es el producto de las desviaciones de los valores X e Y respecto de sus valores medios. En el denominador tenemos las desviaciones cuadráticas medias de X y de Y.
El coeficiente de correlación puede valer cualquier número comprendido entre -1 y +1.
- Cuando r=1, la correlación lineal es perfecta, directa.
- Cuando r=-1, la correlación lineal es perfecta, inversa
- Cuando r=0, no existe correlación alguna, independencia total de los valores X e Y
Variantes de la regresión lineal
La función potencial
y=c·xa
Se puede trasformar en
log y=a·log x+log c
Si usamos las nuevas variables X=log x e Y=log y, obtenemos la relación lineal
Y=aX+b.
Donde b=log c
Ejemplo:
| x | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| y | 1.06 | 1.33 | 1.52 | 1.68 | 1.81 | 1.91 | 2.01 | 2.11 |
Usar la calculadora para transformar esta tabla de datos en esta otra
| X=log x | 1.0 | 1.30 | 1.477 | 1.60 | 1.699 | 1.778 | 1.845 | 1.903 |
| Y=log y | 0.025 | 0.124 | 0.182 | 0.225 | 0.258 | 0.281 | 0.303 | 0.324 |
Calcular mediante el programa regresión lineal los parámetros a y c.
Función exponencial
y=c·eax
Tomando logaritmos neperianos en los dos miembros resulta
ln y=ax+ln c
Si ponemos ahora X=x, e Y=ln y, obtenemos la relación lineal
Y=aX+b
Donde b=ln c.
Ejemplo:
| x | 12 | 41 | 93 | 147 | 204 | 264 | 373 | 509 | 773 |
| y | 930 | 815 | 632 | 487 | 370 | 265 | 147 | 76 | 17 |
Usar la calculadora para transformar esta tabla de datos en esta otra
| X= x | 12 | 41 | 93 | 147 | 204 | 264 | 373 | 509 | 773 |
| Y=ln y | 6.835 | 6.703 | 6.449 | 6.188 | 5.913 | 5.580 | 4.990 | 4.330 | 2.833 |
Calcular mediante el programa regresión lineal los parámetros a y c.
La clase Regresion
En la clase Regresion que describe la regresión lineal los miembros datos son dos arrays x e y que guardan las series de valores X e Y, cuya dependencia funcional deseamos determinar. En los miembros dato públicos a y b se guarda la pendiente de la recta de regresión y la ordenda en el origen.
La función miembro lineal, calcula la pendiente a, y la ordenada en el origen b de la recta de regresión. Se hace uso de variables auxiliares para guardar resultados intermedios: sx guarda la suma de todas las abscisas, sy la suma de todas las ordenadas, sx2 la suma de los cuadrados de las abscisas, sy2 la suma de las cuadrados de las ordenadas, y pxy, la suma de los productos de cada abscisa por su ordenada. Los valores calculados a partir de las fórmulas respectivas, se guardan en los miembros públicos a y b de la clase Regresion.
Para obtener el coeficiente de correlación hemos de calcular primero el valor medio <x> de la serie de datos X, y el valor medio <y> de Y. No calculamos las desviaciones cuadráticas medias sino que empleamos una expresión equivalente a la dada anteriormente para el coeficiente de correlación.
public class Regresion {
private double[] x;
private double[] y;
private int n; //número de datos
public double a, b; //pendiente y ordenada en el origen
public Regresion(double[] x, double[] y) {
this.x=x;
this.y=y;
n=x.length; //número de datos
}
public void lineal(){
double pxy, sx, sy, sx2, sy2;
pxy=sx=sy=sx2=sy2=0.0;
for(int i=0; i<n; i++){
sx+=x[i];
sy+=y[i];
sx2+=x[i]*x[i];
sy2+=y[i]*y[i];
pxy+=x[i]*y[i];
}
a=(n*pxy-sx*sy)/(n*sx2-sx*sx);
b=(sy-a*sx)/n;
}
public double correlacion(){
//valores medios
double suma=0.0;
for(int i=0; i<n; i++){
suma+=x[i];
}
double mediaX=suma/n;
suma=0.0;
for(int i=0; i<n; i++){
suma+=y[i];
}
double mediaY=suma/n;
//coeficiente de correlación
double pxy, sx2, sy2;
pxy=sx2=sy2=0.0;
for(int i=0; i<n; i++){
pxy+=(x[i]-mediaX)*(y[i]-mediaY);
sx2+=(x[i]-mediaX)*(x[i]-mediaX);
sy2+=(y[i]-mediaY)*(y[i]-mediaY);
}
return pxy/Math.sqrt(sx2*sy2);
}
}
|
Uso de la clase Regresion
Una fábrica de bebidas refrescantes observa que sus temperaturas (x) y las ventas (y) de la calle han sido.
| x | 5 | 7 | 10 | 12 | 16 | 20 | 23 | 27 | 19 | 14 |
| y | 9 | 11 | 15 | 16 | 20 | 24 | 27 | 29 | 22 | 20 |
Los datos los guardamos en dos arrays denominados temperatura y ventas
double[] temperatura={5, 7, 10, 12, 16, 20, 23, 27, 19, 14};
double[] ventas={9, 11, 15, 16, 20, 24, 27, 29, 22, 20};
Creamos un objeto regresion de la clase Regresion, pasándole al constructor los dos arrays..
Regresion regresion=new Regresion(temperatura, ventas);
Se llama desde el objeto regresion a su función miembro lineal, para calcular los coeficentes a y b.
regresion.lineal();
System.out.println("Pendiente "+regresion.a);
System.out.println("Ordenada en el origen "+regresion.b);
Se llama también, a la función miembro correlacion, la cual devuelve el coeficiente de correlación
System.out.println("Indice de correlación "+regresion.correlacion());
El proyecto está formado por dos ficheros Regresion.java y Aplicacion.java
public class Aplicacion {
public static void main(String[] args) {
double[] temperatura={5, 7, 10, 12, 16, 20, 23, 27, 19, 14};
double[] ventas={9, 11, 15, 16, 20, 24, 27, 29, 22, 20};
Regresion regresion=new Regresion(temperatura, ventas);
regresion.lineal();
System.out.println("Pendiente "+regresion.a);
System.out.println("Ordenada en el origen "+regresion.b);
System.out.println("Indice de correlación "+regresion.correlacion());
}
} |
El applet que traza la recta de regresión
Este applet representa los datos experimentales y traza la recta de regresión
