El principio de Fermat
A partir del principio del tiempo mínimo de Fermat, se puede obtener las leyes de la reflexión y de la refracción de un modo muy sencillo.
Este principio afirma, que la trayectoria real que sigue un rayo de luz entre dos puntos es aquella en la que emplea un tiempo mínimo en recorrerla.
Ley de la reflexión
Sea una fuente S que emite rayos que se reflejan en una superficie horizontal reflectante y llegan al observador situado en el punto P. Como la luz se propaga en el mismo medio homogéneo, para encontrar la trayectoria que sigue un rayo de luz tal que emplee un tiempo mínimo en recorrerla, equivale encontrar la trayectoria cuya longitud es mínima.
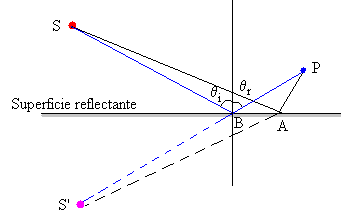 Imaginemos que un rayo emitido por S se refleja en A y
llega a P. La longitud del camino seguido por este rayo es SAP, y esta
longitud es igual a S’AP, siendo S’ la fuente puntual S reflejada en la
superficie. Esta línea es quebrada y por tanto, de mayor longitud que la
línea recta S’BP, que tiene igual longitud que SBP.
Imaginemos que un rayo emitido por S se refleja en A y
llega a P. La longitud del camino seguido por este rayo es SAP, y esta
longitud es igual a S’AP, siendo S’ la fuente puntual S reflejada en la
superficie. Esta línea es quebrada y por tanto, de mayor longitud que la
línea recta S’BP, que tiene igual longitud que SBP.
Para la línea SBP, el ángulo de incidencia θi (que forma el rayo incidente, con la normal a la superficie reflectante) es igual al ángulo de reflexión θr (que forma el rayo reflejado con dicha normal.
Ley de la refracción
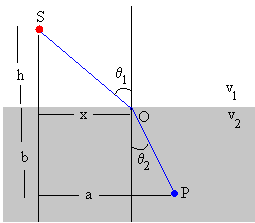 Calculamos el tiempo que tarda un rayo de luz en ir de
la fuente S hasta llegar al observador P. El primer tramo SO lo recorre
en el primer medio con velocidad v1, y el segundo
tramo OP lo recorre en el segundo medio con una velocidad v2.
Calculamos el tiempo que tarda un rayo de luz en ir de
la fuente S hasta llegar al observador P. El primer tramo SO lo recorre
en el primer medio con velocidad v1, y el segundo
tramo OP lo recorre en el segundo medio con una velocidad v2.
El tiempo t es una función de la posición x de O. La función t(x) tendrá un mínimo en la posición x en la que se cumple que la derivada primera de t respecto de x a cero
Esto es equivalente a escribir
Que es la ley de Snell de la refracción
Ejemplo:
Introducimos los valores de las velocidades
-
en el primer medio (amarillo) v1=1.0;
-
en el segundo medio (azul claro) v2=4.0
Pulsamos el botón titulado Nuevo
Medimos en las escalas graduadas las posiciones de S, (punto de color azul en la parte superior) y P (punto de color azul en la parte inferior)
- Posición del emisor S (2.4, 3.3)
- Posición del observador P (-3.1, -2.0)
Movemos con el puntero del ratón el cuadrado de color rojo hasta la posición x=-1.8
Se pulsa el botón titulado Traza
El tiempo que emplea la luz en recorrer el camino SOP es
Se mueve el cuadrado de color rojo a otra posición, y se vuelve a pulsar el botón titulado Traza. Así, hasta encontrar la trayectoria real seguida por un rayo de luz entre la posición S y la P.
Para la posición x=1.6 encontramos la trayectoria real SOP que sigue el rayo de luz.
El ángulo θ1 que forma el rayo incidente con la normal a la superficie de separación es
Comprobamos la ley de Snell de la refracción
Actividades
Se introduce
-
La velocidad de la luz en el primer medio v1, en el control de edición titulado Velocidad A
-
La velocidad de la luz en el segundo medio v2, en el control de edición titulado Velocidad B
Se pulsa el botón titulado Nuevo
Se representa la fuente S en la parte superior y el observador P en la parte inferior. Sus posiciones se asignan aleatoriamente dentro de ciertos límites.
La posición x del punto O, en la superficie de separación entre los dos medios, se puede modificar moviendo con el puntero del ratón un pequeño cuadrado de color rojo.
Se pulsa el botón titulado Trayectoria.
Se traza el camino SOP y se calcula el tiempo que tarda la luz en recorrerlo. Se mueve el punto O hacia la izquierda o hacia la derecha hasta encontrar la trayectoria real SOP seguida por el rayo de luz. Para ayudarnos en esta tarea, se proporciona en la parte superior izquierda del applet, el tiempo empleado por el rayo de luz en recorrer la trayectoria actual y el tiempo empleado por el rayo de luz en recorrer la trayectoria anterior.
Cuando se encuentra la trayectoria SOP real que sigue el rayo de luz, se representa el rayo incidente, el refractado y se proporcionan los datos del ángulo de incidencia y de refracción.
Arrastre con el puntero del ratón el pequeño cuadrado de color rojo
