Dos osciladores acoplados
Experiencia en el aula
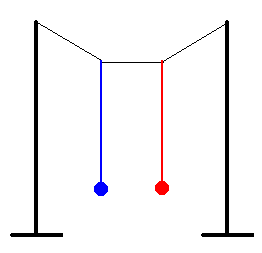 Una experiencia con osciladores
acoplados que se realiza en el aula suele sorprender a los estudiantes. Consiste en
una cuerda que se sujeta por sus extremos situados a la misma altura. Se atan dos
péndulos iguales, a dos puntos simétricos de la cuerda, tal como se indica en la figura.
Se desplaza uno de los péndulos, por ejemplo el de color rojo, de su posición de
equilibrio y se suelta.
Una experiencia con osciladores
acoplados que se realiza en el aula suele sorprender a los estudiantes. Consiste en
una cuerda que se sujeta por sus extremos situados a la misma altura. Se atan dos
péndulos iguales, a dos puntos simétricos de la cuerda, tal como se indica en la figura.
Se desplaza uno de los péndulos, por ejemplo el de color rojo, de su posición de
equilibrio y se suelta.
El péndulo empieza a oscilar pero su amplitud disminuye con el tiempo, el otro péndulo de color azul que estaba inicialmente en reposo, empieza a oscilar con una amplitud que aumenta.
Al cabo de un cierto tiempo, el péndulo rojo se para momentáneamente, y el péndulo azul oscila con la máxima amplitud. Luego, se cambian los papeles, el péndulo azul disminuye su amplitud con el tiempo, y el péndulo rojo va aumentando su amplitud.
Se analiza la situación desde el punto de vista energético, cómo la energía fluye de un péndulo al otro a través del acoplamiento. Si el acoplamiento es débil, como es éste el caso, la suma total de las energías de los dos péndulos debe ser constante.
Ecuaciones del movimiento
Para estudiar un sistema formado por dos osciladores acoplados, vamos a tomar como modelo el sistema formado por dos partículas iguales de masa m situadas en los extremos de dos muelles de idéntica constante elástica k. El acoplamiento se efectúa uniendo las dos partículas mediante un muelle de constante kc, tal como se puede ver en la figura.
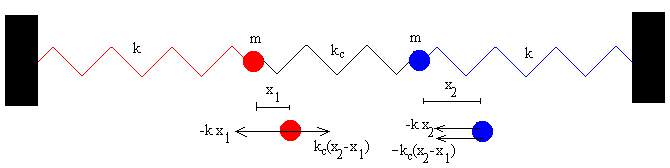
Llamemos x1 y x2 a los desplazamientos de cada una de las partículas a partir de su posición de equilibrio, medidos como positivos cuando están a la derecha. El muelle de la izquierda se ha estirado x1, el de la derecha se ha comprimido x2 y el central se ha deformado x2-x1. Las fuerzas sobre cada una de las partículas se indican en la figura.
- Sobre la partícula de la izquierda, se ejerce una fuerza hacia la izquierda –kx1, y una fuerza hacia la derecha debido a la deformación del muelle central kc(x2-x1), suponemos que x2 es mayor que x1.
- Sobre la partícula derecha, se ejerce una fuerza hacia la izquierda –kx2 y otra fuerza hacia la izquierda debido a la deformación del muelle central –kc(x2-x1).
El muelle central ejerce fuerzas iguales y de sentido contrario sobre cada una de las partículas.
Aplicamos la segunda ley de Newton a cada una de las partículas, y escribimos las ecuaciones del movimiento en forma de ecuaciones diferenciales de segundo orden
Sumando y restando las dos ecuaciones diferenciales tenemos, la ecuación diferencial de un MAS.
Dos movimientos armónicos simples de frecuencias
Las soluciones de estas dos ecuaciones, son respectivamente
Ψa=x1+x2=Ψ0a sin(ωat+φa)
Ψb=x1-x2=Ψ0b sin(ωbt+φb)
Donde las amplitudes Ψ0a y Ψ0b y las fases iniciales φa y φb están determinadas por las condiciones iniciales: posición inicial y velocidad inicial de cada una de las partículas.
Despejando x1 y x2 de las dos ecuaciones anteriores tenemos
El movimiento general de dos osciladores acoplados puede considerarse como la superposición de dos modos normales de oscilación de frecuencias angulares ωa y ωb.
Condiciones iniciales
En el instante t=0, las posiciones iniciales de las partículas son respectivamente x01 y x02. Las velocidades iniciales son cero.
Las ecuaciones se transforman después de algunas operaciones en
Modos normales de vibración
El primer modo normal de vibración de frecuencia ωa se obtiene cuando los dos osciladores se mueven en fase x01 es igual a x02. El muelle central no sufre ninguna deformación y por tanto, no ejerce ninguna fuerza sobre las partículas, las cuales se mueven como si no estuvieran acopladas.
El segundo modo normal de frecuencia ωb se obtiene cuando los dos osciladores se mueven en oposición de fase x01 =- x02. Las ecuaciones del movimiento de cada oscilador se reducen a las siguientes.
Simulación de la experiencia en el aula
Supongamos que x02 es cero, tal como se hace en la demostración de aula. Las ecuaciones del movimiento de las partículas se pueden escribir de forma más simple usando las relaciones trigonométricas cosA+cosB y cosA-cosB.
Cuando la amplitud de un oscilador varía con el tiempo, se denomina amplitud modulada. La amplitud del primer oscilador x01 cos(ωa-ω b )/2 es una función coseno que está adelantada π/2 respecto de la amplitud modulada del segundo oscilador, que es una función seno. Debido a la diferencia de fase entre las dos amplitudes modulantes hay un intercambio de energía entre los dos osciladores. Durante un cuarto de periodo modulante, la amplitud de un oscilador disminuye y la del otro aumenta, dando lugar a una transferencia de energía del primero al segundo. Durante el siguiente cuarto de periodo, la situación se invierte y la energía fluye en dirección opuesta. El proceso se repite continuamente.
Estudio energético
Calculemos la energía total del sistema, la suma de las energías cinética y potencial. Tenemos la energía cinética de cada una de las partículas, la energía potencial elástica del muelle izquierdo que se deforma x1, del muelle derecho que se deforma x2, y del muelle central que se deforma x2-x1.
Una vez agrupados los términos, el primer paréntesis depende solamente de x1, y puede llamarse energía del primer oscilador, el segundo término depende solamente de x2, y puede llamarse energía del segundo oscilador. El último término, que depende de x1 y x2 se denomina energía de acoplamiento o de interacción. Este término es el que describe el intercambio de energía entre los dos osciladores.
Actividades
Se introduce:
- la constante elástica de los dos osciladores, en el control de edición titulado k de los muelles.
- la constante elástica del muelle central, en el control de edición titulado k del acoplamiento
- la masa de las partículas se ha tomado como la unidad.
- la posición inicial de la partícula de la izquierda (una cantidad menor o igual que la unidad), en el control de edición titulado Posición inicial de 1
- la posición inicial de la partícula de la derecha, en el control de edición titulado Posición inicial de 2.
- las velocidades iniciales se toman como cero.
Se pulsa el botón titulado Empieza
Modos normales de vibración
- Primer modo normal de oscilación: introducir la misma cantidad, por ejemplo, 1.0 en los controles de edición titulados Posición inicial 1 y Posición inicial 2.
- Segundo modo normal: introducir la misma cantidad pero con signos opuestos en dichos controles de edición, por ejemplo, 1.0 en Posición inicial 1, y –1.0 en Posición inicial 2.
Simulación de la práctica de aula
- Introducir en el control de edición titulado Posición inicial 1, la cantidad de 1.0, e introducir en el control de edición titulado Posición inicial 2, la cantidad de 0.0.
- Observar, las oscilaciones de las dos partículas, medir el tiempo que tarda un oscilador desde que su amplitud se hace cero hasta que vuelve a hacerse cero. En la parte superior izquierda de la ventana del applet se da el valor del tiempo, y en la parte inferior se representa el desplazamiento de cada partícula en función del tiempo. Usar los botones Pausa y Paso, para aproximarse a los instantes en los que el oscilador elegido se detiene momentáneamente.
- Calcular las frecuencias angulares ωb y ωa de los dos modos de vibración y la frecuencia angular de la amplitud modulada (ωa-ωb)/2, el periodo y el semiperiodo. Comparar el resultado obtenido con las medida efectuada, ¿coinciden?.
