El oscilador forzado que rebota
Dadas las condiciones iniciales apropiadas se puede determinar el movimiento de un cuerpo si conocemos las fuerzas que actúan sobre el mismo. Esto es lo que hemos hecho para determinar la posición de una partícula unida a un muelle elástico en diversas condiciones (sin rozamiento, con rozamiento, sometido a una fuerza oscilante).
Un sistema que experimenta un movimiento caótico nunca se repite a sí mismo, sino que más bien se comporta de forma continuamente diferente, el movimiento puede parecer totalmente aleatorio y desordenado. No obstante, el movimiento caótico está muy lejos de ser totalmente desordenado y por el contrario, exhibe una estructura definida que resulta de pronto aparente. Otro aspecto del caos, es su extrema sensibilidad a las condiciones iniciales.
Podemos describir exactamente el comportamiento de un oscilador forzado por que la fuerza restauradora que ejerce el muelle kx es lineal con respecto al desplazamiento.
Como es natural, todos los muelles reales se desvían de la linealidad para desplazamientos suficientemente grandes, de forma que es inevitable el comportamiento no lineal en el mundo real. Sin embargo, en Física se suelen estudiar casi exclusivamente los sistemas lineales ya que su comportamiento es más simple de describir.
Para hacer que el oscilador forzado sea no lineal, introducimos una barrera que bloquee el movimiento del cuerpo. Se considera que la barrera tiene una masa infinita y que las colisiones del cuerpo oscilante con ella son perfectamente elásticas. Por tanto, lo que hace la barrera es devolver el cuerpo con la velocidad cambiada de signo.
Evidentemente, la fuerza que actúa sobre el cuerpo deja de ser una función lineal del desplazamiento, puesto que la barrera actúa sobre el cuerpo dándole un impulso instantáneo.
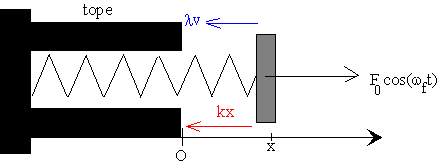
El oscilador forzado
La ecuación diferencial que describe las oscilaciones forzadas es
- donde ω0 es la frecuencia natural o propia del oscilador
- ωf es la frecuencia angular de la fuerza oscilante de amplitud F
- γ es la constante de amortiguamiento, γ<ω0
- δ es el desfase de la fuerza oscilante, que se utilizará más adelante
La solución de la ecuación diferencial es la suma de dos términos:
La solución de la ecuación diferencial homogénea, que describe el estado transitorio y la solución particular que describe el estado estacionario
Introduciendo la solución particular en la ecuación diferencial completa se obtienen los coeficientes A y B
Los coeficientes C y D se determinan a partir de las condiciones iniciales
La velocidad vale
Si las condiciones iniciales son t=0, x=x0, v=v0.
En el estado estacionario
La exponencial exp(-γt) tiende a cero, por lo que
x=Acos(ωf·t)+ Bcos(ωf·t)=A0sin(ωf·t+φ)
A0 es la amplitud de la oscilación forzada en el estado estacionario
Utilizando la fórmula del seno de una suma, tenemos el sistema de ecuaciones
A0·cos φ=A
A0·sin φ=B
El oscilador forzado que rebota en el origen
El choque de la partícula con la barrera hace que su velocidad cambie bruscamente de signo. Para describir su movimiento tenemos que resolver la ecuación diferencial de las oscilaciones forzadas en los intervalos de tiempo entre dos choques consecutivos, tal como se describirá en este apartado.
Primer rebote
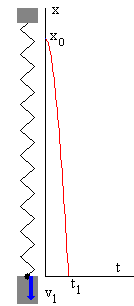 |
El móvil parte en reposo v0=0, desde la posición x0 en el instante t=0, la fase de la fuerza oscilante es δ=0. Conocidas las condiciones iniciales calculamos los coeficientes C y D que describen el estado transitorio La partícula tarda en llegar al origen x=0, un tiempo t1, alcanzando una velocidad v1. |
Determinamos el instante t1 resolviendo la ecuación trascendente
por el procedimiento numérico del punto medio.
Calculamos la velocidad del móvil cuando llega al origen
 |
La partícula rebota elásticamente en la barrera cambiando el sentido de su velocidad de v1<0 a –v1>0. Hasta el próximo choque con la barrera describe una oscilación forzada. Tomamos como cero, el instante en el que rebota, de modo que las condiciones iniciales son: t=0, x0=0, v0=-v1, La fase de la fuerza oscilante no es cero, sino δ=ωf·t1, |
Se determinan los valores de las constantes A, B, C y D de la ecuación de la posición x en función del tiempo t para describir el movimiento de la partícula tras el primer rebote.
En la parte superior de la figura, se muestra la posición de la partícula en función del tiempo, hasta el primer rebote. En la parte inferior, la gráfica de la fuerza oscilante f=F·cos(ωf·t+δ).En el instante t=t1 en el que se produce el primer rebote, la fase de la fuerza oscilante, se muestra en color rojo.
Segundo rebote
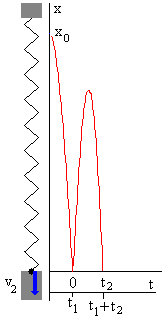 |
La partícula rebota y tarda en volver al origen x=0, un tiempo t2 alcanzando una velocidad v2. Determinamos el instante t2 resolviendo la ecuación trascendente por el procedimiento numérico del punto medio. Calculamos la velocidad del móvil v2 en el instante t2 |
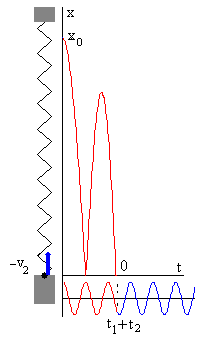 |
La partícula rebota elásticamente en la barrera cambiando el sentido de su velocidad de v2<0 a –v2>0. Tomamos como cero, el instante t=t1+t2 del segundo rebote, de modo que las condiciones iniciales son: t=0, x0=0, v0=-v2, La fase de la fuerza oscilante no es cero, sino δ=ωf·(t1+t2), en color rojo en la figura inferior. |
Se determinan los valores de las constantes A, B, C y D de la ecuación de la posición x en función del tiempo t para describir el movimiento de la partícula tras el segundo rebote.
En la parte superior de la figura, se muestra la posición de la partícula en función del tiempo, hasta el segundo rebote. En la parte inferior, la gráfica de la fuerza oscilante f=F·cos(ωf·t+δ). En el instante t=t1+t2 en el que se produce el segundo rebote, la fase de la fuerza oscilante, se muestra en color rojo.
Tercer rebote
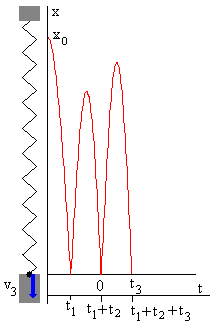 |
La partícula emplea un tiempo t3 en llagar al origen x=0, alcanzando una velocidad v3. Determinamos el instante t3 resolviendo la ecuación trascendente por el procedimiento numérico del punto medio. Calculamos la velocidad del móvil v3 en el instante t3 y así, sucesivamente. |
Ejemplos:
Estudiamos un oscilador forzado
-
La frecuencia natural de oscilación es ω0=0.5 rad/s
-
La amplitud de la fuerza oscilante es F/m=0.25 N/kg
-
La constante de amortiguamiento γ=0.125 s-1
-
La fase de la fuerza oscilante es δ=0
Soltamos la partícula desde una altura x0=2.0 m con velocidad v0=0 en el instante t=0.
Ejemplo 1:
En la figura, se muestra el comportamiento del oscilador cuando la frecuencia de la fuerza oscilante es ωf=1.28 rad/s
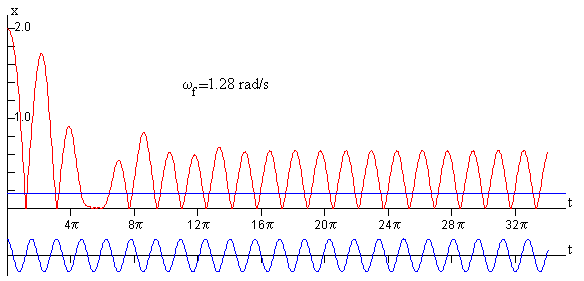
En la parte inferior, la curva de color azul es la fuerza oscilante f=F·cos(ωf·t)
La recta de color azul en la parte superior es la amplitud A0 del oscilador forzado en el estado estacionario para la frecuencia ωf=1.28 rad/s de la fuerza oscilante.
La curva de color rojo, describe el comportamiento del oscilador que rebota. Después de un estado transitorio que dura algunas oscilaciones, la partícula rebota hasta alcanzar una única altura máxima, esta altura es mayor que la amplitud A0 de la oscilación forzada en el estado estacionario. El movimiento de la partícula se repite después de cada rebote, el sistema precisa de un único rebote para completar un ciclo.
Ejemplo 2:
En la figura, se muestra el comportamiento del oscilador cuando la frecuencia de la fuerza oscilante es ωf=1.33 rad/s
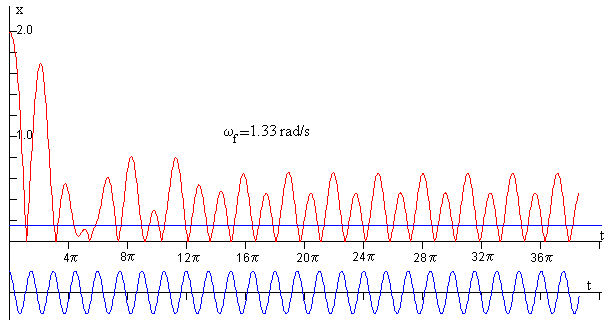
La curva de color rojo, describe el comportamiento del oscilador. Después de un estado transitorio que dura varias oscilaciones, la partícula rebota hasta dos alturas diferentes. El sistema precisa de dos rebotes para completar un ciclo.
Aumentamos un poco la frecuencia ωf, y observamos que en el estado estacionario se alcanzan cuatro alturas máximas distintas, el sistema precisa de cuatro rebotes para completar un ciclo, y así sucesivamente...
Ejemplo 3:
En la figura, se muestra el comportamiento del oscilador cuando la frecuencia de la fuerza oscilante es ωf=1.41 rad/s
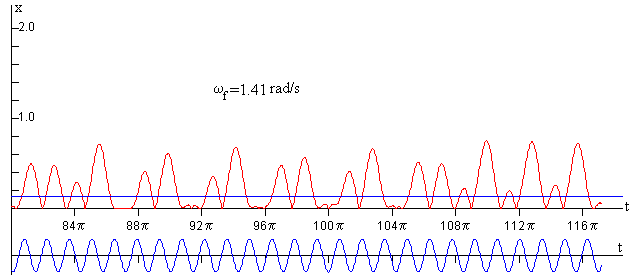
La curva de color rojo, describe el comportamiento del oscilador. Dejamos que el oscilador rebote muchas veces (dependiendo del valor de la constante de amortiguamiento γ), para asegurarnos que se ha alcanzado el estado estacionario, observamos que la partícula rebota hasta múltiples alturas diferentes. El movimiento del sistema nunca se repite es caótico, el periodo es infinito.
Actividades
Se introduce
-
La constante de amortiguamiento γ, en el control de edición titulado Amortiguamiento
-
La amplitud F de la fuerza oscilante, en el control de edición titulado Amplitud fuerza
-
La frecuencia ωf (rad/s) de la fuerza oscilante, actuando en la barra de desplazamiento titulada Frecuencia fuerza
-
La frecuencia propia o natural del oscilador se ha fijado en ω0=0.5 rad/s
-
La posición inicial x0, desde la que se suelta la partícula, con velocidad inicial v0=0, en el control de edición titulado Posición inicial
Se pulsa el botón titulado Empieza
Se observa el movimiento de la partícula unida al muelle elástico, y la representación gráfica de su posición en función del tiempo (en color rojo)
Una flecha de color rojo al lado de la partícula muestra el módulo, dirección y sentido de la fuerza oscilante en cada instante. Una flecha de color azul, representa el vector velocidad. Cuando la fuerza y la velocidad tienen el mismo sentido, el oscilador gana energía, cuando tienen sentidos contrarios pierde energía. Imaginemos un niño en un columpio, cuando le empujamos en la dirección y sentido de su movimiento, el columpio gana energía y aumenta su amplitud. Cuando lo empujamos cuando viene hacia nosotros el columpio pierde energía y disminuye su amplitud.
En la parte inferior del applet, se representa la fuerza oscilante f=F·cos(ωf·t)
Se sugiere al lector que, observe el comportamiento de la partícula para varios valores de la frecuencia ωf·de la fuerza oscilante.
Manteniendo fija, la frecuencia ωf· de la fuerza oscilante, se puede cambiar la posición inicial x0 de la partícula y observar su efecto en su movimiento posterior.
Respuesta en amplitud
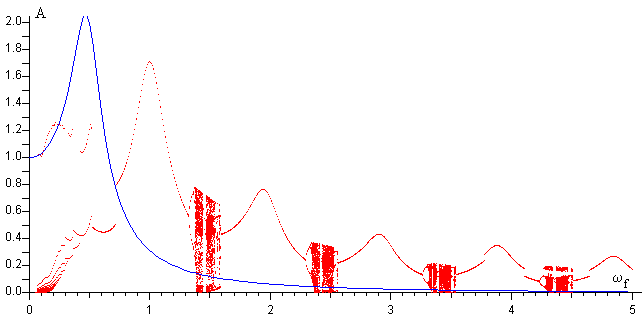
En el applet (más abajo), se dibuja en color azul la respuesta en amplitud del oscilador lineal forzado, es decir, la variación de la amplitud con la frecuencia ωf de la fuerza oscilante, y en color rojo, la respuesta en amplitud del oscilador forzado que rebota.
En el primer caso, vemos que la amplitud alcanza un máximo en las cercanías de de la frecuencia propia ω0=0.5 rad/s.
En el segundo caso, definimos la amplitud como el máximo desplazamiento de la partícula entre dos rebotes consecutivos. La curva presenta un máximo para la frecuencia ωf=1.0 rad/s, y también otros picos secundarios, pero el aspecto más sobresaliente, es la presencia de intervalos de frecuencia donde la amplitud no es única.
Para obtener esta curva se ha procedido del siguiente modo: se deja a la partícula rebotar 100 veces para asegurarnos, que se ha alcanzado el estado estacionario. Después, se representa la máxima altura que alcanza la partícula cuando rebota sucesivamente 200 veces con la barrera para cada una de las frecuencias ωf.
Cuando se elige el intervalo 0<ωf <5, se observan, de un vistazo, las regiones (intervalos de frecuencias) donde la partícula, rebota alcanzando una única altura máxima, de aquellas en las que alcanza múltiples alturas, donde los puntos están verticalmente dispersos. Por tanto, observamos que un sistema físico simple, el oscilador forzado que rebota, presenta un comportamiento complejo.
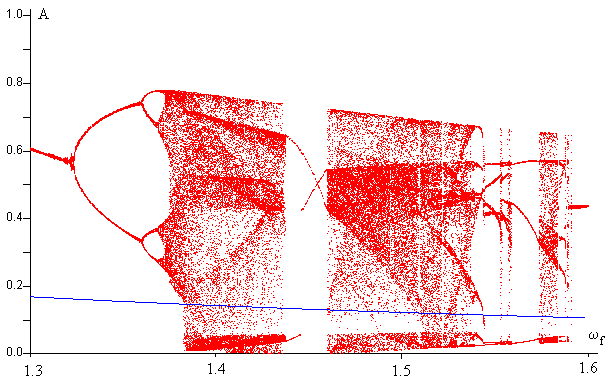
En la figura, se representa la región 1.3< ωf <1.6, observamos que hasta ωf=1.32, la partícula alcanza una única altura máxima. Luego, alcanza dos alturas máximas, la curva que representa la amplitud se bifurca, después cuatro, a partir de ωf =1.36 rad/s, finalmente, múltiples alturas máximas. Observamos también, que hay un intervalo de frecuencias para las cuales no se observan puntos dispersos, sino cierta regularidad en el comportamiento de la partícula.
Actividades
Se introduce
- El intervalo de frecuencias de la fuerza oscilante, en los controles de edición titulados ωf… hasta…
- La escala, que permite amplificar la representación gráfica, verticalmente.
Se ha fijado,
- La frecuencia propia o natural del oscilador en ω0=0.5 rad/s
- La constante de amortiguamiento γ=0.125 s-1
- La amplitud de la fuerza oscilante, F/m=0.25 N/kg
Se pulsa el botón titulado Empieza
Se aconseja examinar en primer lugar, el intervalo (0, 5), después elegir un intervalo más pequeño, por ejemplo (1.3, 1.6), (4.2, 4.5), etc. Cuando la frecuencia es más grande, se aprecia mejor la distribución de puntos que representan la máxima altura alcanzada por la partícula en cada rebote, incrementando la escala vertical.
Referencias
Walker J. S., Soule T. Chaos in a simple impact oscillator: The Bender bouncer. Am. J. Phys. 64 (4) April 1996, pp. 397-409
Tipler. Física. Editorial Reverté (1994). Capítulo 12, págs. 397-402
