El goteo de un grifo
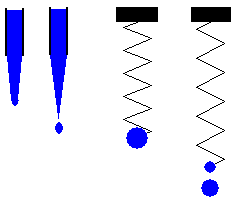 |
El goteo de un grifo es uno de los ejemplos más interesantes que muestran la conducta caótica de los osciladores no lineales. Un modelo sencillo constituido por una masa variable unida a un muelle elástico, describe las características esenciales de este sistema complejo. |
 |
 |
 |
Descripción del modelo
Las ecuaciones que describen el modelo son
Esta ecuación, es similar a la de un oscilador amortiguado bajo la acción del peso mg de la gota de agua.
-
x es el desplazamiento de la gota de agua
-
m es la masa del gota de agua, que va creciendo con el tiempo
-
k es la constante del muelle
-
β es la constante de amortiguamiento
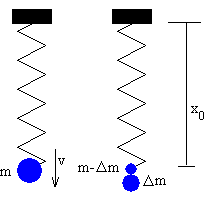 La masa de la gota m no es constante sino
que crece debido al flujo Φ de agua que circula por la tubería.
La masa de la gota m no es constante sino
que crece debido al flujo Φ de agua que circula por la tubería.
El amortiguamiento β, se debe al movimiento del agua en la gota y al flujo Φ de agua. Su expresión es
β= β1+ β2Φ
donde β1 y β2 son constantes
La gota va descendiendo a medida que incrementa su tamaño, cuando alcanza una altura x0, el hilo de agua que la sostiene ya no es capaz de soportar el peso de la gota y se rompe, desprendiéndose una masa Δm de agua que viene dada por la siguiente expresión
Cada vez que se desprende una gota, las condiciones iniciales que determinan la evolución de la siguiente son:
- Posición inicial x0
- Velocidad inicial dx/dt=0
- Masa inicial m0=m-Δm
Se resuelve la ecuación diferencial por el procedimiento de Runge-Kutta con los siguientes valores de los parámetros, tomados del artículo citado en las referencias.
| Parámetro | Valor (unidades arbitrarias) |
| k | 0.01 |
| β1 | 0.0003 |
| β2 | 0.1 |
| α | 0.0286 |
| x0 | 0.03 |
En la simulación, se mantienen fijos estos parámetros y se puede cambiar el flujo Φ supuesto constante, en el intervalo comprendido entre10·10-6 y 100·10-6 unidades arbitrarias.
La primera gota
Para resolver la ecuación diferencial tenemos que asignar unos valores iniciales, en el instante t=0, a la posición, velocidad y masa del sistema que va producir después de un cierto tiempo el desprendimiento de la primera gota.
- Posición inicial x=0.02
- Velocidad inicial dx/dt=0
- Masa inicial m0=1.0·10-6
La evolución de la primera gota, no debe ser tenida en cuenta, al haberse calculado con condiciones iniciales arbitrarias. Son las sucesivas gotas más allá de las iniciales, las que se deben de tener en consideración. Véase el apartado Dependencia del estado inicial de la página titulada Bifurcaciones y régimen caótico.
Representación gráfica
El diagrama de fases
En el diagrama de fases, se representa
-
en el eje vertical, la posición x del móvil
-
en el eje horizontal, la velocidad del móvil dx/dt en cada instante
Esta representación es muy útil en el estudio de los movimientos periódicos
Cuando un oscilador vuelve a la posición inicial x0 con la velocidad de partida después de un tiempo P igual al periodo de la oscilación, describe una trayectoria cerrada en el espacio de las fases, tal como hemos observado en el estudio de las oscilaciones libres. Sin embargo, en las oscilaciones amortiguadas la trayectoria del móvil en el espacio de las fases es una curva abierta, una espiral que tiende hacia el origen, ya que el oscilador no regresa al estado inicial de partida.
El mapa de Lorentz,
En el mapa de Lorentz, se representa:
-
en el eje horizontal el intervalo de tiempo Tn entre el desprendimiento de las gotas n-1 y n
-
en el eje vertical, el intervalo de tiempo Tn+1 entre el desprendimiento de las gotas consecutivas n y n+1.
Si todos los intervalos de tiempo Ti son iguales, el mapa de Lorentz consta de un solo punto. Si hay dos periodos, obtenemos un mapa con dos puntos, y así sucesivamente.
Si los tiempos Ti cambian aleatoriamente como en el régimen caótico, obtenemos un conjunto de puntos.
Actividades
Se introduce
-
El flujo Φ, actuando sobre la barra de desplazamiento titulada Flujo.
-
Se selecciona el tipo de gráfico, activando el botón de radio correspondiente
Se pulsa el botón titulado Empieza.
Ejemplos:
Introducimos un valor del flujo Φ=35·10-6 seleccionando el número 35, moviendo el dedo de la barra de desplazamiento con el puntero del ratón.
Observamos la evolución de las primeras gotas, que como se ha afirmado no se debe de tener en cuenta. Después de que se hayan desprendido varias gotas:
-
Observamos que la trayectoria en el espacio de las fases es una curva cerrada
-
El mapa de Lorentz consta de un solo punto (se excluye las tres primeras gotas)
Introducimos un valor para el flujo de Φ=20·10-6 seleccionando el número 20 en la barra de desplazamiento.
-
Observamos que en el diagrama de las fases, aparecen dos curvas próximas que corresponden a dos oscilaciones de distinto periodo, cuyos valores podemos ver en la parte superior derecha del applet.
-
En el mapa de Lorentz, aparecen dos puntos (se excluyen las tres gotas iniciales).
Introducimos un valor para el flujo de Φ=46·10-6 seleccionando el número 46 en la barra de desplazamiento.
-
Observamos que en el diagrama de las fases, se dibuja varias curvas que corresponden a otros tantas oscilaciones de periodos distintos.
-
En el mapa de Lorentz, aparecen un conjunto de puntos que parecen situarse sobre una curva.
Referencias
Schmidt T., Marhl M. A simple mathematical model of a dripping tap. Eur. J. Phys. 18 (1997), 377-383
