Oscilaciones forzadas. El estado estacionario
Como hemos estudiado en la página anterior, la amplitud de una oscilación amortiguada decrece con el tiempo. Al cabo de un cierto tiempo teóricamente infinito, el oscilador se detiene en el origen. Para mantener la oscilación es necesario aplicar una fuerza oscilante.
Descripción
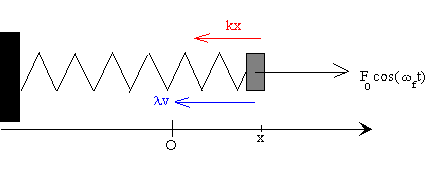
Las fuerzas que actúan sobre la partícula son:
- La fuerza que ejerce el muelle -k·x
- La fuerza de rozamiento proporcional a la velocidad λv y de sentido contrario a ésta
- La fuerza oscilante F0·cos(ωf t) de frecuencia angular ωf
La ecuación del movimiento de la partícula es
ma=-kx-λv+F0·cos(ωf t)
Expresamos la ecuación del movimiento en forma de ecuación diferencial
La solución de esta ecuación diferencial se compone de la suma de dos términos:
- el estado transitorio que depende de las condiciones iniciales y que desaparece al cabo de cierto tiempo, teóricamente infinito.
- el estado estacionario, independiente de las condiciones iniciales, y que es el que permanece, después de desaparecer el estado transitorio.
Una solución particular de la ecuación diferencial completa tiene la forma
Obtendremos los valores de A y δ haciendo que cumpla la ecuación diferencial lineal completa
En la figura, se muestra la respuesta en amplitud de la oscilación forzada, en el estado estacionario. Como podemos observar en la gráfica, la amplitud de la oscilación forzada en el estado estacionario disminuye rápidamente cuando la frecuencia ωf de la fuerza oscilante se hace mayor que la frecuencia propia del oscilador ω0.
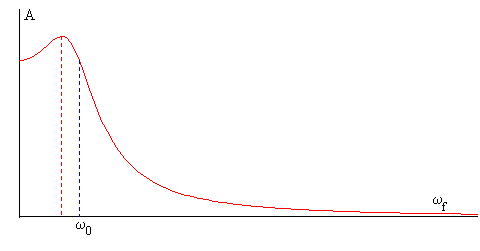
Derivando la expresión de la amplitud A en función de la frecuencia de la fuerza oscilante, respecto de ωf, e igualando a cero, obtenemos la frecuencia ωf para la cual la amplitud en el estado estacionario presenta un máximo
- En
el caso ideal de que no existiese rozamiento γ=0, la amplitud de la oscilación forzada se haría muy
grande, tendería a infinito, cuando la frecuencia ωf de la fuerza oscilante es igual a la frecuencia propia del
oscilador ω0.
- En el caso habitual de que exista rozamiento (γ>0), la amplitud se hace máxima cuando la frecuencia ωf de la fuerza oscilante es próxima a la natural del oscilador ω0
La característica esencial del estado estacionario, es que la velocidad de la partícula
está en fase δ=0 con la fuerza oscilante cuando la frecuencia de la fuerza oscilante ωf es igual a la frecuencia propia del oscilador ω0.
Energía del oscilador forzado. Resonancia
Denotemos por valor medio de una función periódica f(t) de periodo P a
Calculemos el valor medio de la energía por unidad de tiempo suministrada por la fuerza oscilante
El valor medio de la energía por unidad de tiempo que disipa el oscilador a causa de su interacción con el medio que le rodea. Dicha interacción se describe en términos de una fuerza de rozamiento proporcional a la velocidad λv.
En el estado estacionario
x=A·sin(ωf·t+δ)
v=A·ωf·cos(ωf·t+δ)
Haciendo algunas operaciones, se obtiene la misma expresión para P1 y para P2.
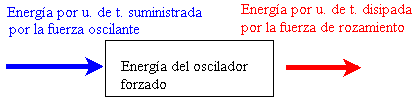
En el estado estacionario, el valor medio de la energía por unidad de tiempo suministrada por la fuerza oscilante, es igual al valor medio de la energía por unidad de tiempo que disipa el oscilador a causa de su interacción con el medio que le rodea. Manteniéndose la energía del oscilador forzado constante en valor medio.
La expresión anterior la podemos escribir de una forma más simple
Cuando la frecuencia ωf de la fuerza oscilante es igual a la frecuencia ω0 natural del oscilador la fuerza oscilante F0·cos(ωf t) y la velocidad v del oscilador están en fase δ=0, el valor medio de la energía por unidad de tiempo P suministrada por la fuerza oscilante es máxima. Esta situación recibe el nombre de resonancia.
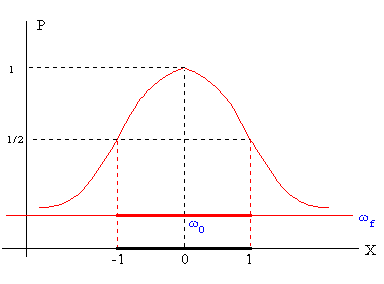 |
La representación de la potencia P en función de X tiene la forma de la curva acampanada de la figura. El máximo de la potencia P se obtiene para X=0, o bien, cuando la frecuencia ωf de la fuerza oscilante es igual a la frecuencia ω0 natural del oscilador. Vemos también que la función es simétrica, tiene el mismo valor para X positivos y X negativos, y que P tiende rápidamente a cero a medida que X se hace mayor o menor que cero, es decir, a medida que la frecuencia ωf de la fuerza oscilante se hace mayor o menor que la frecuencia ω0 propia del oscilador. |
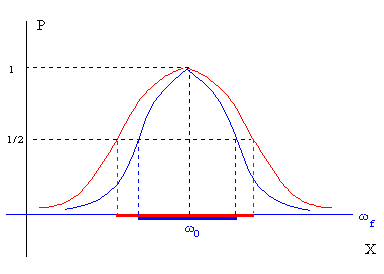 |
La anchura es otra característica
importante de la curva. Se define como el intervalo de frecuencias de la fuerza oscilante
para los cuales la potencia P es mayor que la mitad de la máxima.
El intervalo de frecuencias ωf alrededor de la frecuencia ω0 propia del oscilador
está comprendido entre X=-1 a X=+1, y vale aproximadamente 2γ.
En la figura, se representan dos curvas con la misma frecuencia de resonancia pero con distinta anchura. |
Actividades
Se introduce
- la constante de amortiguamiento γ, en el control de edición titulado Cte. amortiguamiento
- La frecuencia angular ωf de la fuerza oscilante, en el control de edición titulado Frecuencia
- En el programa, se ha fijado el valor de la frecuencia angular natural del oscilador ω0 =100 rad/s, y de la amplitud F0 de la fuerza oscilante.
Se pulsa en el botón Empieza.
En la parte izquierda del applet, se representa la oscilación en el estado estacionario para la frecuencia angular ωf de la fuerza oscilante.
A la derecha del applet, se representa la amplitud y la diferencia de fase en función de la frecuencia ωf de la fuerza oscilante, para un valor de la constante γ de amortiguamiento que se ha introducido. Se señala el valor de la amplitud A y de la diferencia de fase δ para el valor ωf introducido.
