Solución analítica
La ecuación del movimiento es
Cuando x<<l0 la ecuación diferencial se aproxima a

Las condiciones iniciales son: en el instante t=0, la partícula parte de la posición x=A, con velocidad nula, v=dx/dt=0
Integramos esta ecuación diferencial
es el módulo de la velocidad
Como la partícula parte de x=+A y se dirige hacia el origen la velocidad es negativa en el primer cuarto de periodo
Para obtener la posición x del oscilador en función del tiempo t tenemos que integrar nuevamente
Hacemos el cambio de variable
La integral se transforma
La integral elíptica primera especie se define
Se hace el cambio de variable z=sinφ,
se designa am u a la función inversa φ(u)
z=senφ=sin am u=sn u
Esta es la definición de la función elíptica sn.
Análogamente, escribiremos cos am u=cn u
Ambas funciones están relacionadas
sn2 u+cn2 u=1
En el caso que estamos analizando
Conocido el valor de la variable auxiliar z=sn u, se despeja la posición x
Periodo del movimiento
El tiempo que tarda en describir un cuarto de periodo P es
Haciendo el cambio de variable x=Acosφ
El último término es la integral elíptica completa de
primera especie para
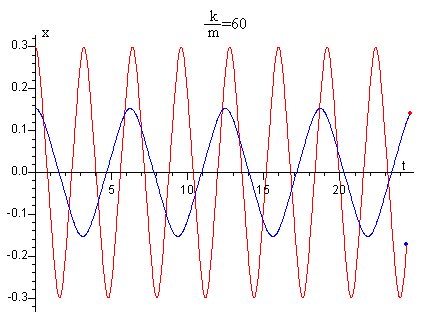
En la figura, se muestra cómo el periodo P depende de la amplitud A
-
La curva en color azul, la amplitud es A=0.15, el periodo es P=3.19 s
-
La curva en color rojo, la amplitud es A=0.3, el periodo es P=6.38 s
Actividades
Se introduce
-
El valor del cociente k/m actuando en la barra de desplazamiento titulada Cociente.
-
La longitud del muelle sin deformar se ha fijado en el programa interactivo en el valor l0=1
Se pulsa el botón titulado Inicio
-
Se desplaza con el puntero del ratón la partícula a una posición inicial A comprendida entre 0.1 y 0.4, de la que parte la partícula con velocidad inicial nula.
Se pulsa el botón titulado Empieza
El programa interactivo calcula la posición x en función del tiempo t, mediante la función elíptica cn
Referencias
Mohazzabi P. Theory and examples of intrinsically nonlinear oscillators. Am. J. Phys. 72 (4) April 2004, pp. 492-498
Detcheva V., Spassov V., A simple nonlinear oscillator: analytical amd numerical solution. Phys. Educ. 28 (1993) pp. 39-42
Puig Adam P., Curso teórico práctico de Cálculo Integral aplicado a la Física y Técnica. Editorial Biblioteca Matemática 1972, págs. 71-76
