Movimiento circular
 Se define movimiento circular como aquél cuya trayectoria es una circunferencia. Una
vez situado el origen O de ángulos describimos el movimiento circular mediante las
siguientes magnitudes.
Se define movimiento circular como aquél cuya trayectoria es una circunferencia. Una
vez situado el origen O de ángulos describimos el movimiento circular mediante las
siguientes magnitudes.
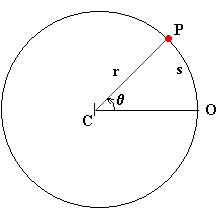
En el instante t el móvil se encuentra en el punto P. Su posición angular viene dada por el ángulo θ, que hace el punto P, el centro de la circunferencia C y el origen de ángulos O.
| Posición angular | θ(t) |
| Velocidad angular | |
| Aceleración angular |
Dada la velocidad v(t) calcular el desplazamiento del móvil θ-θ0 del móvil entre los instantes t0 y t.
Dada la aceleración a(t) calcular el cambio de velocidad ω-ω0 que experimenta el móvil entre los instantes t0 y t
Movimiento circular uniforme
Un movimiento circular uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero.
Movimiento circular uniformemente acelerado
Un movimiento circular uniformemente acelerado es aquél cuya aceleración es constante.
Relación entre las magnitudes lineales y angulares.
La relación entre las magnitudes angulares y lineales es la siguiente:
Longitud del arco s=r·θ
Velocidad, v=ω·r .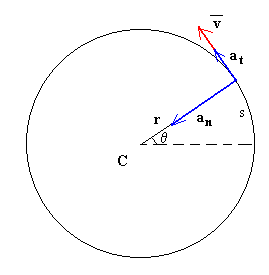 La dirección de la velocidad de un móvil que describe un movimiento circular es
tangente a la trayectoria circular.
La dirección de la velocidad de un móvil que describe un movimiento circular es
tangente a la trayectoria circular.
Un móvil tiene aceleración tangencial at=α·r siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera y es de sentido contrario, si se frena. Un móvil que describe un movimiento circular uniforme no tiene aceleración tangencial.
Un móvil que describe un movimiento circular siempre tiene aceleración normal, an=ω2r ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe.
La aceleración del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración.
