Impulso, momento de una fuerza, momento angular
Impulso
Consideremos el movimiento en una dimensión
La definición de fuerza es
Si la masa es constante, integrando
|
 |
Momento de una fuerza
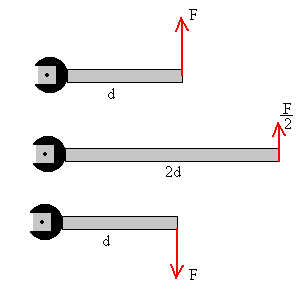Supongamos que tenemos tres llaves que actúan sobre tres tornillos en la forma
indicada por las figuras. Se aplica una fuerza F en el extremo de la llave. Es
fácil contestar a las siguientes preguntas:
- ¿En qué situaciones se enrosca el tornillo?
- ¿En que situaciones se desenrosca el tornillo?
- ¿Cuáles producen el mismo resultado o son equivalentes?.
En la primera figura, el tornillo avanza en una dirección perpendicular al plano de la página, y hacia el lector. El módulo del momento es F·d.
En la segunda figura, el tornillo avanza en la misma dirección y sentido. El módulo del momento es F/2·(2d)=F·d. Con una llave más larga estamos en una situación más favorable que con una llave más corta.
En la tercera figura, el tornillo avanza en la misma dirección pero en sentido contrario.
- Un momento se considera positivo, si el tornillo sale, avanza hacia el lector, la llave gira en sentido contrario al movimiento de las agujas del reloj.
- Un momento se considera negativo, si el tornillo entra, la llave gira en el sentido del movimiento de las agujas del reloj.
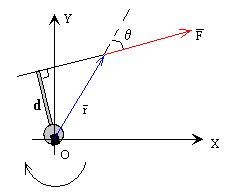
Se denomina momento de una fuerza respecto de un punto, al producto vectorial del vector posición r de la fuerza por el vector fuerza F.
M=r×F
El vector M tiene
- Por módulo, M=F·r·sinθ=F·d. Siendo del brazo de la fuerza (la distancia desde el punto O a la dirección de la fuerza)
- Dirección, perpendicular al plano determinado por la fuerza F y el punto O.
- Sentido, la aplicación de la regla del sacacorchos
La analogía de la llave y el tornillo, nos ayuda a entender el
significado físico de la magnitud momento, y a determinar correctamente el módulo, la
dirección y el sentido del momento de una fuerza:
- El módulo es el producto de la fuerza F por la longitud d de la llave. M=F·r·sinθ=F·d
- La dirección, es la del eje del tornillo, eje Z
- El sentido viene determinado por el avance del tornillo (hacia dentro, negativo) cuando hacemos girar a la llave.
Ejemplos
 |
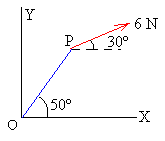Hallar el momento (módulo dirección y sentido) de la fuerza F de módulo 6 N respecto del origen. El punto P de aplicación de la fuerza se encuentra a 45 cm del origen. |
 |
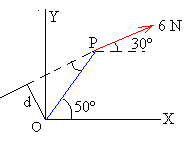Brazo de la fuerza, d=0.45·sin20º
|
Momento angular
|
Se define momento angular L respecto de un punto O como el vector producto vectorial L=r×p=r×mv (la dirección del vector velocidad v es tangente a la trayectoria) El cálculo del momento angular es similar al del momento de una fuerza respecto de un punto, sutituyendo el vector fuerza por el vector momento lineal. |