Rebotes elásticos de una pelota entre dos paredes paralelas horizontales
En esta página, aplicaremos los principios de conservación del momento angular y de la energía para estudiar los sucesivos rebotes elásticos de una pelota entre dos paredes paralelas horizontales y en ausencia de la gravedad. Estudiaremos el comportamiento de la pelota cuando cambia su momento de inercia, es decir, la distribución de masa en su interior y veremos que son posibles movimientos periódicos.
Choque con una pared horizontal
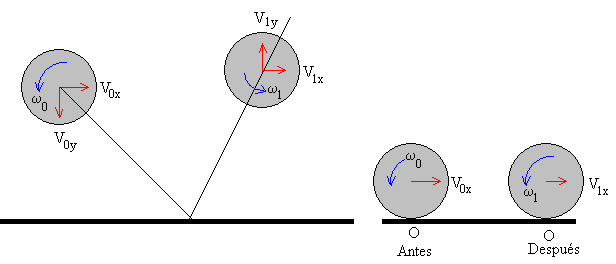
Consideremos una pelota de masa m y radio R, su momento de inercia es es I=γmR2 respecto de un eje que pasa por el centro y es perpendicular al plano de la trayectoria (de la figura) del centro de masas.
- Inmediatamente antes del choque, el centro de la pelota tiene una velocidad cuya componente horizontal es V0x y cuya componente vertical es V0y. La velocidad angular de rotación de la pelota es ω0.
- Inmediatamente después del choque, el centro de la pelota tendrá una velocidad cuya componente horizontal es V1x y cuya componente vertical es V1y. La velocidad angular de rotación de la pelota será ω1.
Supondremos que:
- La componente vertical de la velocidad no cambia de módulo pero cambia de sentido después del choque.
- En el momento del choque, la fuerza que ejerce la pared sobre la pelota actúa en el punto de contacto O. Por lo que el momento angular de la pelota respecto de dicho punto permanece constante.
- Se conserva la energía cinética (choque elástico)
Despejamos V1x y ω1 en el sistema de dos ecuaciones con dos incógnitas
Después del primer choque, las velocidades V1x y Rω1 se expresan en términos de las velocidades iniciales V0x y Rω0
Choque con la pared opuesta
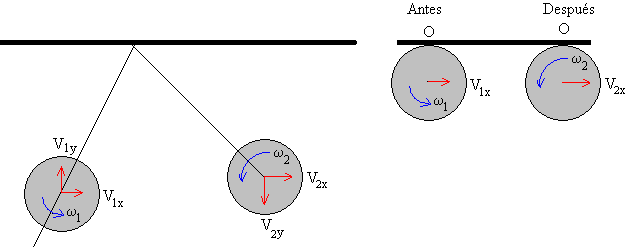
- La componente vertical de la velocidad no cambia de módulo pero cambia de sentido después del choque.
- En el momento del choque, la fuerza que ejerce la pared sobre la pelota actúa en el punto de contacto O. Por lo que el momento angular de la pelota respecto de dicho punto permanece constante.
- Se conserva la energía cinética (choque elástico)
Despejamos V1x y ω1 en el sistema de dos ecuaciones con dos incógnitas
Después del segundo choque, las velocidades V2x y Rω2 se expresan en términos de las velocidades V1x y Rω1 de la pelota después del primer choque.
Sucesivos choques
Después del segundo choque, la pelota se dirige hacia la primera pared, las ecuaciones (1) nos permiten calcular V3x, V3y, Rω3 en términos de V2x, V2y, Rω2. Después del tercer choque, la pelota se dirige hacia la pared opuesta, las ecuaciones (2) nos permiten calcular V4x, V4y, Rω4 en términos de V3x, V3y, Rω3 y así, sucesivamente.
Se puede despejar la componentes de la velocidad del centro de la pelota Vnx y Vny y la velocidad angular de rotación Rωn después de n choques en términos de las correspondientes velocidades iniciales V0x, V0y, Rω0 (véase Tavares)
Si la distribución de masa es tal que θ=2π/k donde k es un entero k≥4 los valores de las velocidades se repiten.
Por ejemplo, para k=4, (γ=1) Vnx y ωn se repiten después de cuatro choques con las paredes.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Vx | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 |
| Rω | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 |
| Vx | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 | 1 |
| Rω | 0 | -1 | 0 | 1 | 0 | -1 | 0 | 1 | 0 |
La trayectoria se repite después de cuatro choques
Para k=5 (γ≈0.52786), Vnx se repite después de cinco choques y ωn se repiten después de diez choques.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Vx | 1 | -0.38 | -1.24 | -0.38 | 1 | 1 | -0.38 | -1.24 | -0.38 | 1 | 1 | -0.38 |
| Rω | 1 | -1.62 | 0 | 1.62 | -1 | -1 | 1.62 | 0 | -1.62 | 1 | 1 | -1.62 |
| Vx | 1 | 0.31 | -0.81 | -0.81 | 0.31 | 1 | 0.31 | -0.81 | -0.81 | 0.31 | 1 | 0.31 |
| Rω | 0 | -1.31 | 0.81 | 0.81 | -1.31 | 0 | 1.31 | -0.81 | -0.81 | 1.31 | 0 | -1.31 |
La trayectoria se repite después de diez choques
Para k=6 (γ=1/3), Vnx se repite después de seis choques y ωn se repiten después de tres choques.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Vx | 1 | 0 | -1 | -1 | 0 | 1 | 1 | 0 |
| Rω | 1 | -2 | 1 | 1 | -2 | 1 | 1 | -2 |
| Vx | 1 | 0.5 | -0.5 | -1 | -0.5 | 0.5 | 1 | 0.5 |
| Rω | 0 | -1.5 | 1.5 | 0 | -1.5 | 1.5 | 0 | -1.5 |
La trayectoria se repite después de seis choques
Utilizando las fórmulas (3) para k=5 (γ≈0.52786), las velocidades después del n=6 choque son
- Para las condiciones iniciales: V0x=1, Rω0=1
V6x=-0.382, Rω0=1.618
- Para las condiciones iniciales: V0x=1, Rω0=0
V6x=0.309, Rω0=1.309
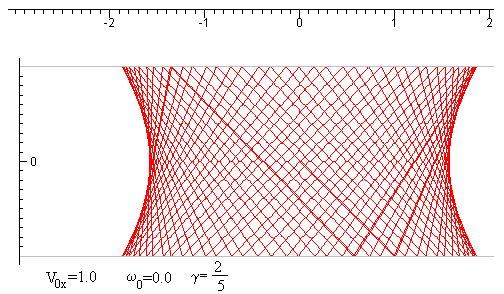
En la figura, se representa la trayectoria del centro de la pelota (una esfera γ=2/5) después de rebotar muchas veces con las paredes horizontales.
Actividades
Se introduce
- La velocidad inicial horizontal, V0x, actuando en la barra de desplazamiento titulada V. Horizontal Vx
- La velocidad inicial de rotación, ω0, actuando en la barra de desplazamiento titulada V. Rotación ω.
- El coeficiente γ del momento de inercia I=γmR2 de la pelota, en el control de edición titulado gamma
- La velocidad inicial vertical se ha fijado en V0y=-1
- El radio de la pelota se ha fijado en R=1
Se pulsa el botón titulado Empieza
Observar el movimiento de la pelota y anotar las velocidades iniciales V0x, Rω0 de la pelota y las velocidades Vnx, Rωn después de cada choque n.
Referencias
Tavares J. M. The elastic bounces of a sphere between two parallel walls. Am. J. Phys. 75 (8) August 2007. pp. 690-695
