Equilibrio de una barra
En esta página, se explica el concepto de momento de una fuerza y se aplica al equilibrio de una barra horizontal apoyada en un extremo.
Momento de una fuerza
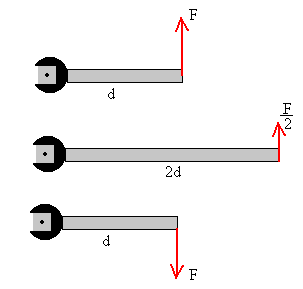 Supongamos que tenemos tres llaves que actúan sobre tres tornillos en la forma
indicada por las figuras. Se aplica una fuerza F en el extremo de la llave. Es
fácil contestar a las siguientes preguntas:
Supongamos que tenemos tres llaves que actúan sobre tres tornillos en la forma
indicada por las figuras. Se aplica una fuerza F en el extremo de la llave. Es
fácil contestar a las siguientes preguntas:
- ¿En qué situaciones se enrosca el tornillo?
- ¿En que situaciones se desenrosca el tornillo?
- ¿Cuáles producen el mismo resultado o son equivalentes?.
En la primera figura, el tornillo avanza en una dirección perpendicular al plano de la página, y hacia el lector. El módulo del momento es F·d.
En la segunda figura, el tornillo avanza en la misma dirección y sentido. El módulo del momento es F/2·(2d)=F·d. Con una llave más larga estamos en una situación más favorable que con una llave más corta.
En la tercera figura, el tornillo avanza en la misma dirección pero en sentido contrario.
- Un momento se considera positivo, si el tornillo sale, avanza hacia el lector, la llave gira en sentido contrario al movimiento de las agujas del reloj.
- Un momento se considera negativo, si el tornillo entra, la llave gira en el sentido del movimiento de las agujas del reloj.
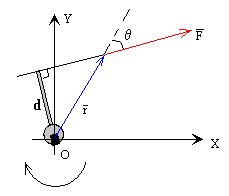
Se denomina momento de una fuerza respecto de un punto, al producto vectorial del vector posición r de la fuerza por el vector fuerza F.
M=r×F
El vector M tiene
- Por módulo, M=F·r·sinθ=F·d. Siendo del brazo de la fuerza (la distancia desde el punto O a la dirección de la fuerza)
- Dirección, perpendicular al plano determinado por la fuerza F y el punto O.
- Sentido, la aplicación de la regla del sacacorchos
 La analogía de la llave y el tornillo, nos ayuda a entender el
significado físico de la magnitud momento, y a determinar correctamente el módulo, la
dirección y el sentido del momento de una fuerza:
La analogía de la llave y el tornillo, nos ayuda a entender el
significado físico de la magnitud momento, y a determinar correctamente el módulo, la
dirección y el sentido del momento de una fuerza:
- El módulo es el producto de la fuerza F por la longitud d de la llave. M=F·r·sinθ=F·d
- La dirección, es la del eje del tornillo, eje Z
- El sentido viene determinado por el avance del tornillo (hacia dentro, negativo) cuando hacemos girar a la llave.
Ejemplos
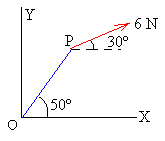 |
Hallar el momento (módulo dirección y sentido) de la fuerza F de módulo 6 N respecto del origen. El punto P de aplicación de la fuerza se encuentra a 45 cm del origen. |
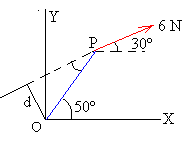 |
Brazo de la fuerza, d=0.45·sin20º
|
Varilla que pende de dos muelles
La varilla delgada de masa m kg y longitud L pende de dos muelles elásticos verticales de constantes k1 y k2 y de longitudes l01 y l02 sin deformar, situados a una distancia d1 y d2 a uno y otro lado del c.m de la varilla
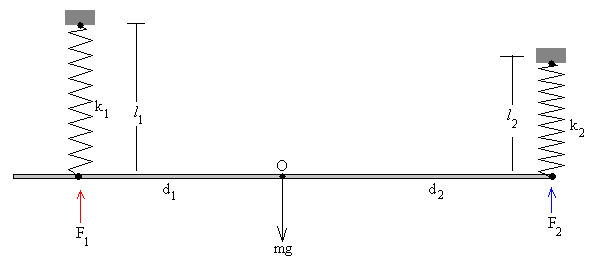
-
La fuerza que ejerce el muelle situado a la izquierda del c.m. es F1=k1x1, donde x1 es la deformación del muelle
-
La fuerza que ejerce el muelle situado a la derecha del c.m. es F2=k2x2, donde x2 es la deformación del muelle
Cuando la varilla está en equilibrio en posición horizontal. La resultante de las fuerzas sobre la varilla debe ser cero y el momento resultante respecto del c.m. debe ser cero.
k1x1+ k2x2=mg
-k1x1·d1+ k2x2·d2=0
Despejamos x1 y x2
-
El muelle de la izquierda se ha de colgar de un punto situado a l1=l01+x1 por encima de la varilla horizontal
-
El muelle de la derecha se ha de colgar de un punto situado a l2=l02+x2 por encima de la varilla horizontal
Ejemplo:
- Constantes elásticas de los muelles: k1=50 N/m, k2=25 N/m
- Masa de la barra, m=1 kg
- Longitud de los muelles sin deformar, l01=l02=0.5 m
Cuando d1=75 cm, d2=90 cm, las deformaciones son
-
El muelle de la izquierda se ha de colgar de un punto situado a l1=50+10.7=60.7 cm por encima de la varilla horizontal
-
El muelle de la derecha se ha de colgar de un punto situado a l2=50+17.8=67.8 cm por encima de la varilla horizontal
Actividades
Se introduce
-
La constante elástica k1 del muelle de la izquierda en N/m, en el control de edición titulado Cte. elástica k1.
-
La constante elástica k2 del muelle de la derecha en N/m, en el control de edición titulado Cte. elástica k2.
-
La masa de la varilla se ha fijado en m=1 kg
-
Las longitudes de los mulles sin deformar se ha fijado en l0=50 cm
Se pulsa el botón titulado Nuevo
-
Con el puntero del ratón se arrastra los pequeños círculos de color rojo, para establecer la posición de enganche de los muelles a la varilla, es decir las distancias d1 y d2 de los muelles al c.m.
Se pulsa el botón Nuevo, arrastrar con el puntero del ratón los pequeños círculos de color rojo
