Choque de dos bolas de billar
Cuando dos bolas de billar chocan, las direcciones de sus velocidades justamente después del choque forman 90º. Sin embargo, deja de cumplirse la condición de que las bolas de billar ruedan sin deslizar, y como consecuencia de ello, la velocidad de su c.m. e incluso sus direcciones cambian durante un cierto tiempo, hasta que se restablece la condición de rodar sin deslizar. Las direcciones finales de las velocidades de las dos bolas dejan de formar 90º.
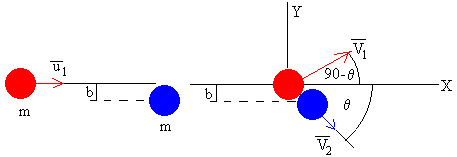
Una bola de billar rueda sin deslizar sobre el tapete con velocidad u1 y choca con una bola de billar idéntica en reposo. Vamos a determinar:
- Las velocidades y direcciones de las bolas de billar inmediatamente después del choque
- El movimiento posterior de las dos bolas de billar mientras deslizan sobre el tapete
- Las velocidades finales constantes de las dos bolas de billar y sus direcciones cuando ruedan sin deslizar.
Choque bidimensional
Supondremos que las dos bolas de billar tienen la misma masa m y el mismo radio R, que el choque es perfectamente elástico, e=1. Despreciamos el efecto del rozamiento entre las superficies de las dos bolas en el breve intervalo de tiempo en el que están en contacto en el momento del choque. Las velocidades de los centros de masa de las dos bolas inmediatamente después del choque y sus direcciones están dadas por las expresiones.
V1=u1·sinθ
V
2=u1·cosθ
b=2R·sinθ
b se denomina parámetro de impacto
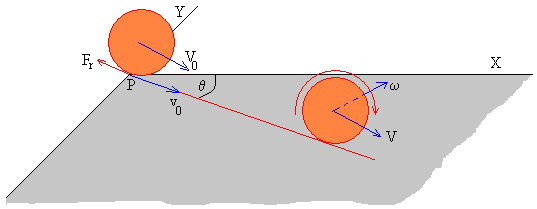
En la figura se muestra, las velocidades del c.m. de las esferas y la velocidad angular de rotación, antes del choque y después del choque. La bola incidente rueda sin deslizar, la velocidad de su c.m. u1 y la velocidad angular de rotación ω1 forman 90º, la relación entre sus módulos es ω1=u1/R.
Después del choque, la velocidad angular de rotación no cambia, pero cambia la velocidad de su c.m. tanto en módulo como en dirección, los vectores V1 y ω1 no forman 90º y la relación entre sus módulos ω1≠V1/R.
Consideremos la bola que estaba inicialmente en reposo, su c.m. adquiere después del choque, una velocidad V2 formando un ángulo θ con el eje X , pero no tiene velocidad angular inicial de rotación, tampoco se cumple la condición de rodar sin deslizar ya que ω2≠V2/R.
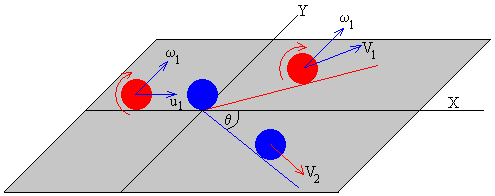
Movimiento de la bola incidente después del choque
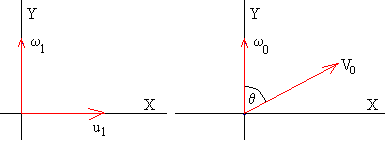
La bola incidente tiene una velocidad u1 y rueda sin deslizar lo largo del eje X, su velocidad angular de rotación vale u1/R y su dirección es el eje Y,
ω1x=0
ω1y=u1/R,
La bola incidente inmeditamente después del choque adquiere una velocidad V0=u1·senθ, y se mueve en una dirección que hace un ángulo 90-θ con el eje X. La velocidad angular de rotación no cambia si despreciamos el efecto del rozamiento entre las superficies de las dos bolas en el breve intervalo de tiempo en el que están en contacto en el momento del choque. Las componentes de la velocidad de su c.m. son
V0x= u1·sin2θ
V0y= u1·sinθ·cosθ
Las componentes de la velocidad angular de rotación son
ω0x=0
ω0y=u1/R

Las componentes de la velocidad del punto P de contacto de la bola con el plano horizontal son,
v0x=V0x-ω0y·R= u1·sin2θ-
u1=-u1·cos2θ
v0y=V0y+ω0x·R = u1·sinθ·cosθ
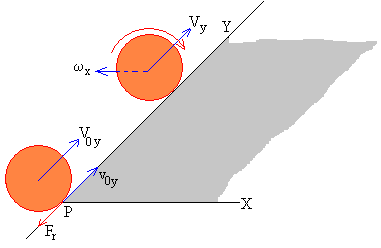
El módulo de la velocidad inicial del punto P vale
v0= u1·cosθ
El movimiento del c.m. es la composición de dos movimientos uniformemente acelerados.
Las componentes de la velocidad del c.m. son
Si la bola parte del origen en el instante t=0, la posición del c.m. en función del tiempo es
Si en el instante t=0, las componentes de la velocidad angular de rotación ω, son ω0x=0 y ω0y=u1/R. Las componentes de la velocidad angular de rotación de la bola en el instante t son
La bola comienza a rodar sin deslizar en el instante t1 en el que la velocidad del punto P de contacto de la bola con el plano horizontal es nula
0=Vx-ωy·R
0=Vy+ωx·R
Despejamos el tiempo t,
La velocidad constante del c.m. de la bola en este instante es
El ángulo que forma el vector velocidad V1 con el eje X es
Las componentes de la velocidad angular de rotación en este instante son
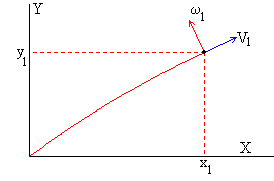 |
Ya que Rω1x=-V1y y Rω1y=V1x. El vector velocidad angular ω, es perpendicular al vector velocidad del c.m. V, ya que el producto escalar ω·V=0 La relación ente sus módulos es V=R·ω |
La posición del c.m. de la bola en este instante es
Movimiento de la bola inicialmente en reposo después del choque
El c.m. de la bola inicialmente en reposo después del choque adquiere una velocidad V0=u1·cosθ, y se mueve en una dirección que hace un ángulo -θ con el eje X. La velocidad angular de rotación ω0 que inicialmente es cero, no cambia si despreciamos el efecto del rozamiento entre las superficies de las dos bolas en el breve intervalo de tiempo en el que están en contacto en el momento del choque.
La bola se mueve a lo largo de la dirección que forma un ángulo θ con el eje X, sin desviarse. La fuerza de rozamiento Fr=μmg disminuye la velocidad del c.m. y aumenta la velocidad de rotación hasta que se cumpla la condición V=ω·R
Como la velocidad inicial de rotación es cero, la velocidad inicial del punto P de contacto de la bola con el plano horizontal vale
v0= u1·cosθ
La fuerza de rozamiento se opone a esta velocidad. La ecuación del movimiento del c.m. es
La velocidad V del c.m. en instante t es
V= u1·cosθ-μg·t
La posición s del c.m. en el instante t es
s= u1·cosθ·t-μg·t2/2
Las coordenadas del c.m. son x=s·cosθ, y=-s·sinθ
Sabiendo que el momento de inercia de una esfera es 2mR2/5
La ecuación de la dinámica de rotación es
La velocidad angular de rotación ω en instante t es
ωR= 5μg·t/2
La bola comienza a rodar sin deslizar en el instante t2 en el que la velocidad del punto P de contacto de la bola con el plano horizontal es nula
0=V-ω·R
Despejamos el tiempo t,
que es el mismo que t1
La velocidad constante del c.m. de la bola de billar es
En el instante t2 la bola se encuentra a una distancia del origen,
a lo largo de la recta que forma un ángulo –θ con el eje X.
Velocidades finales constantes de las dos bolas de billar
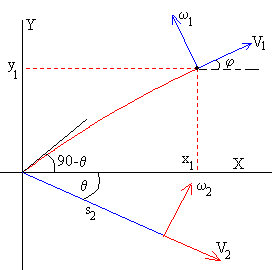 |
El ángulo entre los vectores velocidad V1 y V2 a partir del instante tr=t1=t2 es la suma del ángulo φ que forma el vector V1 con el eje X, y del ángulo θ que forma el vector V2 con el eje X. |
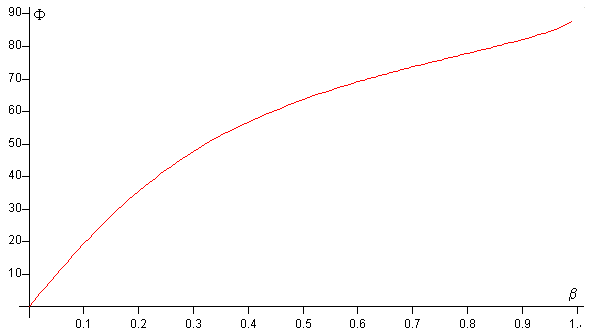
En la figura, se representa este ángulo Φ en función de la fracción β=b/(2R) del parámetro de impacto. Este ángulo difiere de 90º que es el ángulo entre las direcciones de las velocidades de las bolas de billar inmediatamente después del choque.
A partir del instante tr el movimiento de las dos bolas de billar es rectilíneo y uniforme
-
La primera bola
x=x1+V1x(t-tr)
y=y1+V1y (t-tr)
-
La segunda bola
s=s2+V2(t-tr)
a lo largo de la recta que forma un ángulo –θ con el eje X.
Balance energético
Energía inicial antes del choque es la energía cinética de traslación del c.m. de la bola incidente con velocidad u1 y de rotación u1/R alrededor de un eje que pasa por su c.m.
Como el choque es elástico, la energía total no cambia. Disminuye la energía de la bola incidente, y aumenta la energía de la bola que estaba inicialmente en reposo
La energía final de ambas partículas a partir del instante t>tr cuando ambas ruedan sin deslizar con velocidad constante sobre el plano horizontal es
Actividades
Se introduce
-
La velocidad inicial u1, actuando en la barra de desplazamiento titulada Velocidad
-
La fracción b/(2R) del parámetro de impacto, en la barra de desplazamiento titulada P. impacto.
-
El coeficiente de rozamiento μ, en el control de edición titulada Coef. rozamiento.
Se pulsa el botón titulado Empieza
Se observa la trayectoria del c.m. de las dos bolas de billar.
Se dibujan los vectores
-
Velocidad de traslación del c.m. V, en color azul
-
Velocidad angular de rotación, ω·R, en color rojo
-
Velocidad del punto P de contacto de la esfera con el plano horizontal v, en color negro
La velocidad del punto P va disminuyendo hasta que se hace cero, en el instante tr.
Los vectores velocidad angular de rotación ωR, y velocidad de traslación del c.m. V, van cambiando de módulo y dirección hasta que sus direcciones se hacen perpendiculares y sus módulos se igualan.
La dirección del vector V es tangente a la trayectoria.
A partir del instante tr, el c.m. sigue una trayectoria rectilínea, los vectores V, y ωR no cambian de módulo ni de dirección.
En la parte superior izquierda del applet, se proporcionan los datos relativos a la bola de billar incidente- Componentes de la velocidad del c.m. V1x, V1y
- Componentes de la velocidad angular de rotación R·ω1x, R·ω1y
- Componentes de la velocidad del punto P de contacto de la bola con el plano horizontal, v1x, v1y
En la parte inferior izquierda del applet, se proporcionan los datos relativos a la bola que estaba inicialmente en reposo
- La velocidad del c.m. V2, la dirección θ de la velocidad es, senθ=b/(2R), con el eje X.
- La velocidad angular de rotación R·ω2
- La velocidad del punto P de contacto de la bola con el plano horizontal, v2
Se señala la posición de las bolas en el instante tr, cuando las bolas de billar comienzan a rodar sin deslizar, manteniendo su velocidad constante tanto en módulo como en dirección
Referencias
Wallace R. E., Schroeder M. C. Analysis of billiard ball collisions in two dimensions. Am. J. Phys. 56 (9) September 1988, pp. 815-819
