Movimiento de rodar en el plano inclinado (II)
En la página titulada “Movimiento de rodar en un plano inclinado” estudiamos el movimiento de rodar de un cuerpo sólido en forma de aro, cilindro o esfera a lo largo de un plano inclinado.
En la página titulada “Equilibrio rotación-traslación” estudiamos el movimiento de un de un disco que rueda sobre un plano horizontal cuya velocidad inicial de traslación y de rotación podía ser cualesquiera. El papel de la fuerza de rozamiento era el de establecer el equilibrio entre las velocidades de traslación vc del centro de masas y de rotación ω alrededor de un eje que pasa por el c.m., de modo que al cabo de un cierto tiempo se cumpliese que vc=ω·R.
En esta página, vamos a simular una experiencia en la que se combina ambas situaciones.
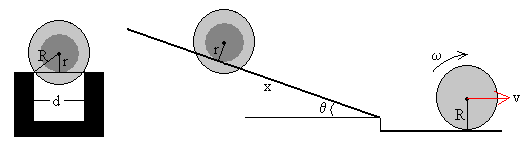
Supongamos una esfera de radio R que baja rodando sin deslizar a lo largo de un carril acanalado cuyas vías están separadas una distancia d<2R, y a continuación, se mueve sobre un plano horizontal. Se tratará de determinar la velocidad final vc del centro de masas (c.m.) de la esfera.
Movimiento sobre un carril inclinado
La esfera tiene dos puntos de contacto con el carril, como podemos apreciar en la figura. Hay por tanto, dos fuerzas de rozamiento Fr y dos reacciones N del carril. La fuerza de rozamiento Fr tiene la dirección del carril, la reacción N es perpendicular al carril y pasa por el centro de la esfera.
-
La resultante de las fuerzas de rozamiento es F1=2Fr
-
La resultante de las dos reacciones iguales y simétricas es N1=2Nr/R.
Siendo r la distancia entre el plano que contiene las dos vías del carril y el centro de la esfera r2=R2-d2/4.
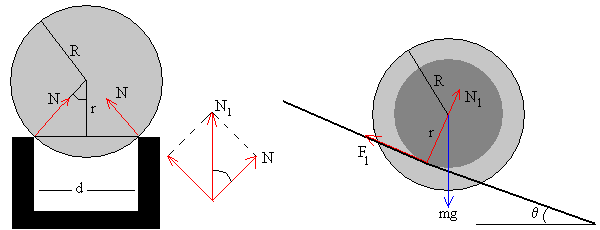
Las fuerzas que actúan sobre la esfera son:
- El peso mg
- La resultante de las reacciones N1
- La resultante de las fuerzas de rozamiento F1
Las ecuaciones del movimiento de la esfera son
- Equilibrio en la dirección perpendicular al plano inclinado
N1=mg·cosθ
- Movimiento de traslación del c.m.
mg·sinθ-F1=mac
- Movimiento de rotación alrededor de un eje que pasa por el c.m.
F1·r=Ic·α
- La esfera rueda sin deslizar si
ac=α·r
Teniendo en cuenta que el momento de inercia de una esfera es Ic=2mR2/5. Despejamos la aceleración del centro de masas
Calculamos la fuerza de rozamiento Fr y la reacción N en cada uno de los puntos de apoyo
Condición de rodar sin deslizar
La esfera rueda sin deslizar siempre que Fr sea menor que la fuerza de rozamiento máxima Fr<μs·N. Teniendo en cuenta que el momento de inercia de la esfera es Ic=2mR2/5. La inecuación se transforma en esta otra equivalente.
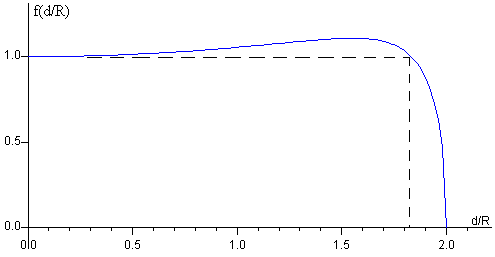
Representamos gráficamente la función f(d/R) que multiplica a
2·tanθ/7. Esta función crece desde el valor
d/R=1.0 hasta alcanzar un máximo en
La fracción es mayor que la unidad para d/R<1.8. Si fijamos el valor del ángulo θ, el coeficiente de rozamiento tiene que ser μs>2·tanθ/7. Por ejemplo, si θ=30º, μs>0.165, siempre que d/R<1.8
Balance energético
Cuando la esfera rueda sin deslizar. La velocidad del c.m. v0 cuando llega al final del plano inclinado de longitud x, es
Cuando la esfera baja rodando sin deslizar, la energía potencial de la esfera se transforma en energía cinética de traslación y de rotación
Despejamos v0 y obtenemos la misma expresión que la deducida a través de las ecuaciones del movimiento.
Movimiento sobre el plano horizontal
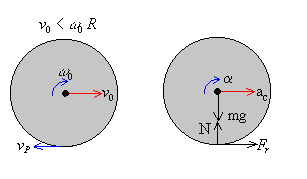 Cuando la esfera se pone en contacto con el plano
horizontal la velocidad de su c.m. es v0 y su velocidad
angular de rotación es ω0=v0/r. Como en
general, r<R no se cumple la condición de rodar sin deslizar v0=ω0·R.
Cuando la esfera se pone en contacto con el plano
horizontal la velocidad de su c.m. es v0 y su velocidad
angular de rotación es ω0=v0/r. Como en
general, r<R no se cumple la condición de rodar sin deslizar v0=ω0·R.
La fuerza de rozamiento actúa sobre el punto de contacto de la esfera con el plano horizontal a fin de restablecer la condición de equilibrio entre ambos movimientos.
Estamos en la situación en el que la velocidad del punto P de contacto de la rueda con el suelo no es nula vp=v0-ω0·R sino que está dirigida hacia la izquierda es decir, vp<0. La fuerza de rozamiento Fr tiene sentido hacia la derecha.
Las ecuaciones del movimiento son
- Equilibrio en sentido perpendicular al plano horizontal
N=mg
- Movimiento de traslación del c.m.
m·ac=Fr
- Movimiento de rotación alrededor de un eje que pasa por el c.m.
Icα =-Fr·R
- Valor de la fuerza de rozamiento que actúa en el punto de contacto P que desliza a lo largo del plano horizontal.
Fr=μk·N
La velocidad v del centro de masa aumenta
vc=v0+μk·gt
La velocidad angular ω de rotación disminuye. Recordando que la velocidad inicial de rotación es ω0=v0/r.
La velocidad del punto P de la esfera en contacto con el plano horizontal es
vP=vc-ω ·R
que se hace cero vP=0, en el instante t.
El desplazamiento s del c.m. y el desplazamiento angular φ, ángulo girado por la esfera en el tiempo t son respectivamente
Movimiento de rodar sin deslizar
En dicho instante t se establece el movimiento de rodar sin deslizar, v=ω ·R.
La velocidad final constante vc del c.m. de la esfera es
Balance energético
Determinamos la relación entre la energía inicial Ei, la final Ef y el trabajo de la fuerza de rozamiento W.
La energía inicial de la esfera es
La energía final de la esfera cuando rueda sin deslizar vc=ω ·R es
La fuerza de rozamiento favorece el movimiento de traslación y se opone al movimiento de rotación. El trabajo de la fuerza de rozamiento es
W=Fr·s-Mr·φ =-mμk g(-s+Rφ)
Hemos calculado anteriormente los valores de los desplazamientos s y φ hasta el instante t en el que el disco rueda sin deslizar. Después de hacer algunas operaciones se obtiene
Podemos comprobar finalmente, que
W=Ef-Ei
Ejemplo:
-
Cociente entre radios, d/R=1.5.
-
Radio de la esfera, R=10 cm
-
Coeficiente de la fuerza de rozamiento del plano horizontal e inclinado, μ=0.45
-
Distancia que recorre la esfera a lo largo del plano inclinado, x=1 m
-
Ángulo del plano inclinado, 30º
r2=R2-d2/4. Tendremos que r=0.066 m
Obtenemos mediante las ecuaciones de la dinámica o del balance energético la velocidad v0 del c.m. de la esfera al abandonar el plano inclinado.
La velocidad angular de rotación de la esfera será es
La esfera comienza a rodar sobre el plano horizontal, pero no se cumple la condición v0=ω0·R. La velocidad del punto P de contacto de la esfera con el plano horizontal no es cero, sino que vale
vP=v0-ω0 ·R=-1.16 m/s
La fuerza de rozamiento tratará de restablecer el equilibrio, entre los movimientos de traslación y rotación hasta que vP=0. Por lo que incrementa la velocidad de traslación vc y disminuye la velocidad angular de rotación ω.
Al cabo de un tiempo de
se restablece el equilibrio y la esfera rueda sin deslizar con una velocidad constante de
Balance energético
La energía inicial de la esfera es
Ei=mgx·senθ=m·9.8·1.0·sen30º=4.9·m J
Esta energía se va trasformando en energía cinética de traslación y de rotación
Como vc=ω·r. Con R=0.1 y r=0.066. La energía cinética de rotación representa el
48% de la energía cinética total
Cuando rueda sin deslizar a lo largo del plano horizontal se cumple vc=ω·R
La energía cinética de rotación representa los 2/7=29% de la energía cinética total
Actividades
Se introduce
- La posición inicial x de la rueda en el plano inclinado, en el control de edición titulado Posición
- El cociente entre el ancho del carril d y el radio R de la esfera, actuando sobre la barra de desplazamiento titulada Cociente ancho/radio.
- El radio R de la esfera está fijado en el programa en 10 cm=0.1 m
- El coeficiente μs= μk de la fuerza de rozamiento del plano horizontal e inclinado, en el control de edición titulado Coef. rozamiento.
- El ángulo del plano inclinado se ha fijado en 30º
Se pulsa el botón titulado Empieza
En el caso de que no se cumpla la condición μ>0.165, para d/R<1.8, el programa no prosigue y un mensaje nos invita a incrementar el coeficiente de rozamiento μ, a fin de que la esfera baje rodando sin deslizar a lo largo del plano inclinado.
Si se cumple la citada condición, se observa el movimiento de la esfera a lo largo del plano inclinado y luego, sobre el plano horizontal.
Cuando la esfera desliza sobre el plano horizontal, la velocidad del punto P de contacto de la esfera con dicho plano no vale cero, vP<0 y va disminuyendo (en módulo) hasta que se cumple la condición de rodar sin deslizar vP=0. Un vector de color rojo muestra el valor de dicha velocidad vP.
En la parte derecha del applet, se muestran las transformaciones energéticas. Cuando la esfera rueda sin deslizar a lo largo del plano inclinado la energía potencial se trasforma en energía cinética de traslación del centro de masas y de rotación alrededor de un eje que pasa por el centro de masas. La fuerza de rozamiento no realiza un trabajo neto.
Cuando se pone en contacto con el plano horizontal, no se cumple en general que vc=ω ·R, por lo que la fuerza de rozamiento tratará de restablecer el equilibrio entre el movimiento de traslación y el de rotación. Durante un cierto tiempo t se pierde energía debido al trabajo de la fuerza de rozamiento. A partir de dicho instante, la velocidad final del c.m.vc se mantiene constante y la fuerza de rozamiento no realiza un trabajo neto.
Referencias
Cromer A. An unusual rolling-sphere phenomenon. The Physics Teacher Vol 34, January 1996, pp. 48-50.
Quing-gong-Song. The requirement of a sphere rolling without slipping down a grooved track for the coeffcient of static friction. Am. J. Phys. 56 (12) December 1988, pp. 1145-1146
