Movimiento de un carrete que rueda
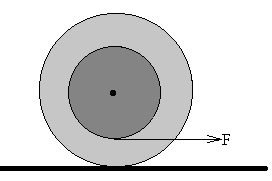 En esta página, continuamos con la discusión del movimiento de rodar
bajo la acción de una fuerza aplicada F. La diferencia con los ejemplos previos es que la fuerza F no
es paralela a la superficie a lo largo de la cual rueda el cuerpo, sino que forma cierto
ángulo
En esta página, continuamos con la discusión del movimiento de rodar
bajo la acción de una fuerza aplicada F. La diferencia con los ejemplos previos es que la fuerza F no
es paralela a la superficie a lo largo de la cual rueda el cuerpo, sino que forma cierto
ángulo
Este ejemplo es especialmente útil para clarificar ciertas cuestiones de mecánica de los cuerpos rígidos que se ponen de manifiesto cuando hacemos la siguiente demostración de aula. Enrollamos un hilo a un carrete y tiramos de su extremo con una fuerza F tal como indica la figura. Preguntamos a los estudiantes. ¿En qué dirección se moverá el carrete, hacia la izquierda o hacia la derecha?.
Fuerza sobre un carrete
Aplicamos una fuerza F al carrete haciendo un ángulo θ con la horizontal tal como se indica en la figura. La fuerza F tiene una componente horizontal F·cosθ .
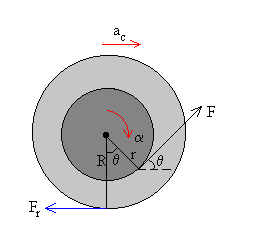 |
Las ecuaciones del movimiento son ahora.
Además de la condición de rodar (sin deslizar) ac=α ·R |
Resolviendo las ecuaciones despejamos las incógnitas ac y Fr.
La fuerza de rozamiento Fr vale
Fr=Fcosθ-mac
La fuerza de rozamiento Fr se anula para un valor del ángulo θ r tal que
El carrete rueda sin fricción independientemente del valor de la fuerza F aplicada, siempre que no supere un valor máximo que se calculará más abajo.
Se producen tres casos
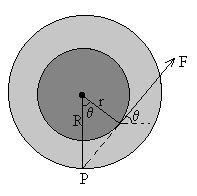
- Equilibrio
Cuando se cumple que cosθ =r/R. La aceleración del c. m. es cero.
Como podemos ver en la figura, la dirección de la fuerza F pasa por el punto P de contacto entre el carrete y la superficie horizontal. El momento de la fuerza aplicada respecto de P es cero, no hay rotación alrededor del eje instantáneo que pasa por P.
El ángulo θc tal que cosθc=r/R, se denomina ángulo crítico
- Se mueve hacia la derecha
Cuando cosθ >r/R, o bien cuando θ <θc, la aceleración ac es positiva y el carrete se mueve hacia la derecha.
- Se mueve hacia la izquierda
Cuando cosθ <r/R, o bien cuando θ >θc, la aceleración ac es negativa y el carrete se mueve hacia la izquierda.
Condición de rodar sin deslizar
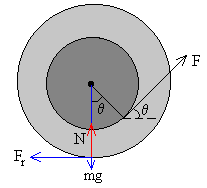 Para cada ángulo θ, hay un límite de la fuerza F que se puede aplicar para que el carrete ruede sin deslizar. Esto
ocurre cuando la fuerza de rozamiento Fr alcanza su máximo
valor Fr=μ·N= μ(mg-F·sinθ)
Para cada ángulo θ, hay un límite de la fuerza F que se puede aplicar para que el carrete ruede sin deslizar. Esto
ocurre cuando la fuerza de rozamiento Fr alcanza su máximo
valor Fr=μ·N= μ(mg-F·sinθ)
Conocida la fuerza de rozamiento Fr, calculamos la fuerza máxima F que podemos aplicar y la aceleración máxima ac.
μ(mg-F·sinθ)=F·cosθ-mac
Sustituyendo ac por su valor y despejando F
Podemos comprobar que para el ángulo θ=θr se cumple que la fuerza máxima que podemos aplicar es F=mg/senθ, y por tanto, la normal N vale cero, el carrete deja de tener contacto con el plano horizontal.
Carrete de forma cilíndrica
Si el carrete es un cilindro de masa m y de radio R, cuyo momento de inercia es Ic=mR2/2.entonces k=3/2
La fuerza de rozamiento Fr se anula para un valor del ángulo θ r tal que
Resumiendo, el carrete tiene una aceleración ac que es positiva si θ <θc y es negativa si θ >θc. El carrete rueda sin deslizar siempre que la fuerza aplicada F no supere un valor máximo que depende del ángulo y del coeficiente estático de rozamiento.
- Para θ =θc el carrete desliza independientemente del valor del coeficiente de rozamiento estático.
- Para θ =θr el carrete rueda sin deslizar, independientemente de que lo pequeño que sea el coeficiente estático de rozamiento.
Ejemplo:
Sea r/R=0.5, el ángulo crítico θc=60º, de modo que si
- Si θ =60º el carrete no se mueve
- Si θ <60º el carrete se mueve hacia la derecha. Por ejemplo si θ =30º,
- ac=3.66 m/s2
- Fr=6.83 N en el sentido indicado por la flecha roja en el punto P de contacto con la superficie.
- Si θ >60º el carrete se mueve hacia la izquierda. Por ejemplo si θ =70º,
- ac=-1.58 m/s2
- Fr=6.71 N en el sentido indicado por la flecha roja en el punto P de contacto con la superficie.
Actividades
Se introduce
- El valor de la fuerza aplicada F, en el control de edición titulado Fuerza
- La dirección de dicha fuerza, el ángulo θ , que forma con la horizontal, actuando en la barra de desplazamiento titulada Ángulo
- La relación entre el radio del tambor r en el que está enrollada la cuerda y el radio del carrete R, en el control de edición titulado Cociente radios.
- La masa está fijada en el programa interactivo m=1 kg
Se pulsa el botón titulado Empieza
En este applet solamente se estudia el movimiento de rodar sin deslizar de un carrete de forma cilíndrica. Se supondrá que la fuerza F aplicada se mantiene siempre por debajo de la fuerza máxima para todos los ángulos comprendidos entre 0 y 180º.
