El oscilador de “Atwood”
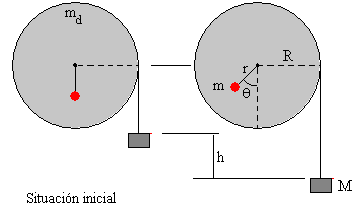
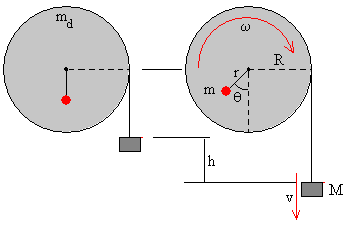
En esta página, se estudia un sistema oscilante, que consiste en un disco de masa md y radio R. que puede girar alrededor de un eje perpendicular al disco y que pasa por su centro. Se pega una masa puntual m a una distancia r de su centro. Se equilibra el sistema, colgando una masa M de una cuerda enrollada al disco, tal como se muestra en la figura.
Equilibrio y estabilidad
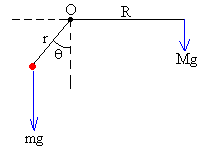 El equilibrio se logra, cuando el momento del peso que
cuelga respecto del eje de rotación del disco, es igual y de sentido
contrario al momento de la masa adicional m pegada al disco a una
distancia r de su eje. El desplazamiento angular de equilibrio θe de la masa puntual es
El equilibrio se logra, cuando el momento del peso que
cuelga respecto del eje de rotación del disco, es igual y de sentido
contrario al momento de la masa adicional m pegada al disco a una
distancia r de su eje. El desplazamiento angular de equilibrio θe de la masa puntual es
MgR=mgr·sinθe
La altura de equilibrio del bloque es he=R·θe
El ángulo θe existe si se cumple que MR≤mr
Estudiamos ahora la situación desde el punto de vista energético.
Consideremos la situación cuando la masa adicional m se ha desplazado un ángulo θ, y el bloque de masa M ha descendido una altura h=R·θ (véase la primera figura)
Ep(θ)=mgr(1-cosθ)-MgR·θ.
Calculamos sus extremos derivando la función energía potencial Ep(θ) respecto del ángulo θ, e igualando a cero.
hay dos posibles ángulos, θe y π-θe. Vamos a comprobar que al primero le corresponde un mínimo de la energía potencial, mientras que al segundo le corresponde un máximo. Hallamos la derivada segunda de la función energía potencial
El coseno es positivo (mínimo) para θe, y negativo (máximo) para π-θe.
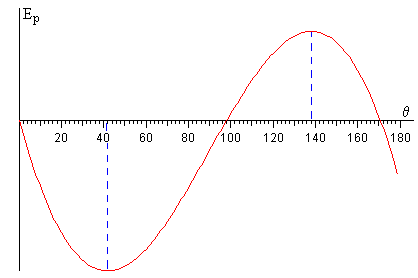
En la figura, vemos que la función Ep(θ) presenta un mínimo para θe=41º, y un máximo para 180- θe=139º
Cuando mr=MR el máximo y el mínimo coinciden en θ=90º que es el punto de inflexión.
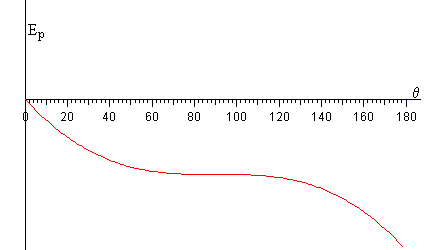
Cuando MR>mr la función energía potencial es una función decreciente de θ.
Ecuación del movimiento
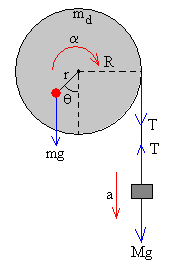 |
En la figura, se muestran las fuerzas que actúan sobre el disco y las fuerzas que actúan sobre el bloque de masa M. El disco gira en el sentido indicado con aceleración angular α, y el bloque lleva una aceleración a. La relación entre ambas aceleraciones es a=α·R
|
El momento de inercia del disco de masa md y de la masa adicional m es
Eliminando la tensión T de la cuerda, llegamos a la ecuación diferencial del movimiento del disco
Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales t=0, θ=0, dθ/dt=0.
Oscilaciones alrededor de la posición de equilibrio estable
Como caso particular, estudiamos las oscilaciones de pequeña amplitud, alrededor de la posición de equilibrio θe
Poniendo θ=θe+φ, en la ecuación diferencial
Desarrollando el seno de una suma, y aproximando sinφ≈φ, cosφ≈1
Que es la ecuación diferencial de un MAS de frecuencia angular
Ejemplo:
-
Masa del disco, md=1 kg
-
Masa puntual pegada al disco, m=0.3 kg
-
Masa del bloque que cuelga, M=0.1 kg
-
Radio del disco R=1 m
-
Distancia de la masa puntual m al centro del disco, r=0.5 m
Ángulos máximo y mínimo
La función energía potencial presenta un mínimo para θe=41.8º, y un máximo para 180- θe=138.2º
El periodo de las oscilaciones de pequeña amplitud alrededor de la posición de equilibrio estable es
En la simulación, el sistema parte del reposo desde la posición θ=0. La energía inicial es cero. Cuando se encuentra en la posición θ=60º=π/3, la energía potencial vale
Ep=0.3·9.8·0.5(1-cos(π/3))-0.1·9.8·1.0·(π/3)=-0.29 J
La energía cinética es la suma de la energía cinética de rotación del disco que se mueve con velocidad angular ω, y la energía cinética del bloque que se mueve con velocidad v. La relación entre ambas velocidades es v= ω·R
Aplicando el principio de conservación de la energía
Ek+Ep=0,
0.3375ω2-0.29=0, ω=0.93 rad/s
La energía potencial vuelve a ser cero en la posición
Ep(θ)=mgr(1-cosθ)-MgR·θ=0. El ángulo θ, se obtiene resolviendo la ecuación trascendente
mr(1-cosθ)-MR·θ=0
1.5(1-cosθ)-θ=0
La raíz es θ=1.71 rad=98º, como podemos apreciar en la primera gráfica.
Actividades
Se pulsa el botón titulado Nuevo
-
Se arrastra con el ratón el punto de color rojo, que representa la masa puntual m pegada al disco, para establecer la distancia r al eje del disco
Se introduce
-
La masa puntual m, en el control de edición titulado Masa izquierda
-
La masa del bloque que cuelga M, en el control de edición titulado Masa derecha
-
El radio del disco se ha fijado en R=1 m
-
La masa del disco se ha fijado en md=1 kg
Se pulsa el botón titulado Empieza
Se dibuja la función energía potencial, observamos el máximo y el mínimo si existen.
A la derecha del applet, observamos el movimiento del sistema, que oscila alrededor de la posición del mínimo de energía potencial si existe, o el bloque cae si no existe posición de equilibrio estable.
Para comenzar una nueva experiencia se pulsa el botón titulado Nuevo
Arrastre con el puntero del ratón el círculo de color rojo
Referencias
Greenslade T. B. “Atwood’s” oscillator. Am. J. Phys. 56 (12) December 1988, pp. 1151-1153
